一種基於 Schnoor 算法的多籤方案以及錢包架構

硬核預警，建議有技術基礎的同學使用～

近日比特幣核心客戶端發布了新的一個大版本，這次發布主要帶來了 Schnorr 籤名 Taproot 技術。Schnorr 是一項優雅，簡潔，可以提升交易隱私性，節省空間，同時還能實現聚合多籤的一種的籤名算法。同時它有別於傳統的 ESDSA 籤名技術，其在技術及實現方式上有着明顯的特點，目前已經較廣泛的應用在不同公鏈的不同環節上。本期非常有幸邀請到密碼學專家漢升（筆名）撰稿，介紹一種基於 Schnoor 算法的多籤方案以及錢包架構。同時在文末為大家推薦了兩篇相關科普文章，希望能夠一起學習這一項新的技術，以及了解 Schnorr 籤名對於比特幣及區塊鏈技術的發展有哪些意義。

ECDSA籤名回顧  

數字籤名是對籤名的數字模擬。最早的數字籤名算法是由Rivest、Shamir、Adleman三⼈於1978年提出的RSA籤名算法，其安全性基於⼤整數分解的難解性，⼴泛地運⽤於數字認證與CA等領域。但是由於RSA算法的密鑰尺⼨較⼤，存儲效率不及後來的基於橢圓曲线的籤名算法。所以⽬前⼴泛運⽤於密碼貨幣的籤名⼏乎都是ECDSA算法，只是所基於的底層橢圓曲线不同。ECDSA的安全性是基於橢圓曲线離散對數難解性。

⽐特幣籤名算法——

基於 SECP256k1 曲线的ECDSA

⽐特幣⽬前所使⽤的籤名算法是基於SECP256k1 曲线的ECDSA算法。將交易的詳細信息 作消息摘要， 即 z=SHA256(m)，對摘要z作核⼼籤名算法。

密碼學意義上安全的數字籤名需要通過添加隨機數來實現籤名的隨機性。但是根據RFC6979標准，籤名 算法中的隨機數是從消息摘要z中提取出，這不是密碼學意義上的隨機數。這個⽅案在衆多密碼學代碼庫中，並應⽤於⼤多數區塊鏈項⽬中。

Schnorr籤名的平凡⽅案

Schnorr籤名可以解決上⾯所提出的多籤消耗資源的問題。

Schnorr是由Claus-Peter Schnorr在1989年美密會上提出的數字籤名算法，並申請了專利保護。就籤名算法本身⽽⾔，它相對於ECDSA算法具有，可證明安全性、可擴展性的特點。

主要算法實現如下：

可以看出Schnorr籤名也基於橢圓曲线算術，⽬前⼴泛部署於各⼤代碼庫、芯⽚指令中的底層算術模塊依 

然可以有效利⽤，但是需要將再重新從底層接⼝封裝指令來實現Schnorr算法。這點對於軟件錢包升級⽐ 較便利。但是對於硬件錢包，升級成本可能較⾼。 

Schnorr籤名⽅案的线性性質

假設Alice和Bob分別對於消息m進⾏籤名。具體地，假設Alice的公私鑰對為(x1,X1=x1G) ，Bob的公私 (x2,X2=x2G),

以上的⽅案只是為了展示Schnorr籤名的线性性，並不能直接⽤於實際應⽤，因為這個⽅案可能會導致 Rouge key Attack。 

基於Schnorr籤名的多籤⽅案

多籤⽅案

以n-of-m多籤⽅案為例。

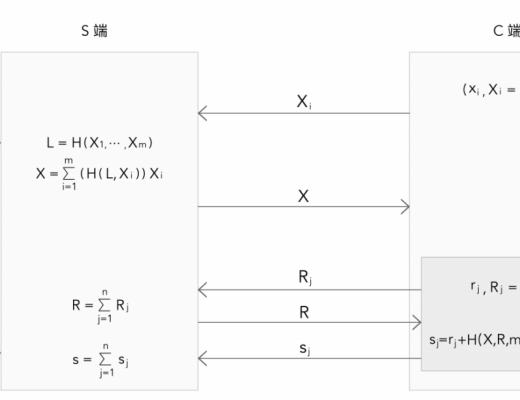
錢包服務架構

錢包分為服務器端(S端)和客戶端(C端)，C端將有多個邏輯點，對應多個⽤戶。

這⾥的S端和C端只是邏輯上的，可以在⼀個物理設備上既有S端也有C端，也可能是多個物理設備上的。 

結論

對於Schnorr的线性性質以及籤名可累積性質，使得在⽐特幣多籤交易的執⾏中，不需要過多的⽤戶籤名數據，只需要"籤名和"與"公鑰和"即可驗證交易合法性。這會讓⽐特幣的多籤交易⼤⼩⼤幅降低，從⽽區塊能容納的多籤交易數量得到較⼤提⾼。以2-3多籤為例，⽬前⽐特幣多籤的鎖定腳本需要3個公鑰地址，這部分會被壓縮為腳本，所以升級之後⼤⼩⽆變化，但是解鎖腳本需要2個公鑰與2個籤名，在升級為Schnorr之後，只需要⼀個"公鑰和"與"籤名和"。對於更通⽤的n-m多籤，⽬前⽐特幣多籤的解鎖腳本需要n個公鑰與n個籤名，Schnorr籤名依然只需要⼀個"公鑰和"與⼀個"籤名和”。也就是說籤名⼈越多，Schnorr籤名的空間利⽤率越⾼。 

推薦閱讀：

技術向：為什么 Schnorr 籤名被譽為比特幣 Segwit 後的最大技術更新

（https://linux.cn/article-12797-1.html）

科普：無處不在的數字籤名

（https://halfrost.com/digital_signature/）

編輯：xy 工作室 、 NPC

鄭重聲明：本文版權歸原作者所有，轉載文章僅為傳播信息之目的，不構成任何投資建議，如有侵權行為，請第一時間聯絡我們修改或刪除，多謝。