比特幣算法進化為Schnorr籤名算法是進步嗎？

歷史的車輪滾滾向前,技術的進步從未停歇，一次具有裏程碑意義特幣協議的开始了它的技術升級。其協議中的技術升級 Schnorr Signature （施諾爾籤名）和 Taproot （樹的主根）已集成到Bitcoin Core 0.21.0 版本中。

比特幣的未來似乎面臨從未有過的光明，現在它有機會不僅通過其容量而且通過其功能超越所有其他區塊鏈。

當比特幣 ECDSA 橢圓曲线籤名算法時，多重籤名交易驗證過程非常繁瑣，現在可以把一筆交易中的所有籤名和公鑰通通合並成單個籤名和公鑰，無法追溯並且簡單快速會是怎樣？

其實在此之前，中本聰在設計比特幣協議時，需要考慮到籤名算法的籤名長度、是否开源、是否有專利、是否經過足夠長時間的安全驗證、性能等多種條件。當時能滿足上述這些條件的數字籤名算法不止有 ECDSA，還有 Schnorr Signature 這個從各個方面都不亞於 ECDSA 的數字籤名算法。但是由於在 2008 年之前處於專利保護的狀態，所以可能是這個原因使得中本聰在設計比特幣協議時並未使用該籤名算法，最終選擇了橢圓曲线數字籤名算法（ECDSA），還在其他專家的建議下選擇了一條特殊的橢圓曲线 secp256k1。

時隔10年，2018 年 7 月，比特幣开發者 Pieter Wuille 撰寫了 bip-schnorr提出了將 bitcoin 的籤名算法更改為 schnorr 方案。Schnorr 與 ECDSA 雖然同為使用 secp236k1 曲线的橢圓曲线加密算法，但由於Schnorr Signature 在密碼學特性上的優勢，可以在幾乎同等安全的基礎上，更方便的構建多籤名交易。

Schnorr 使用在比特幣上，相比ECDSA會有一些額外的顯著優勢：

1. 更安全：在隨機預言模型中很容易證明 Schnorr 籤名的安全性，而 ECDSA 不存在這樣的證明。

2. 無延展性困擾：ECDSA籤名是可延展性的，第三方無需知道私鑰，可以直接修改既有籤名，依然能夠保持該籤名對於此交易是有效的。比特幣一直存在延展性攻擊，直到SegWit激活後才修復，前提是使用segwit交易，而不是傳統交易。BIP62 和 BIP66 對此有詳細描述。

3. 线性：Schnorr籤名算法是线性的！以這一特性作為基礎，可以構建更高效和隱私性更強的區塊鏈系統。使用 Schnorr 籤名的各方可以生成對其各自密鑰的籤名聚合。例如，N個公鑰進行籤名，採用ECDSA的話，則有N個籤名，驗證同樣需要做N次。若使用Schnorr，由於线性特性，則可以進行籤名疊加，僅保留最終的疊加籤名。例如同一個交易無論輸入數量多少，其均可疊加為一個籤名，一次驗證即可。

Schnorr籤名算法幾乎在各個層面均優於比特幣現有的籤名算法ECDSA：性能，安全，體積，擴展性等方面等，並且Schnorr Sig可以與ECDSA使用同一個橢圓曲线：secp256k1 curve，升級起來的改動非常小。

當然在比特幣協議中除了籤名算法之外，還設計了Taproot 腳本語言定義如何使用比特幣。比特幣多籤類地址可以不用暴露出自己的「多籤」身份，也可以支持數量衆多的多籤場景（鏈上交易只需要一個聚合的公鑰和一個籤名），降低很多的交易字節數，特別是對於需要高頻操作的地址而言，降低鏈上的交易費用，可以節省不少的成本。

下面是一些比較常見的問答：

Q&A

Q: Schnorr籤名是否可以用在m of n多重籤名上？
A: 當然可以。多重籤名只是m of n的籤名數量的模式。與籤名算法無關。

Q: Schnorr的組籤名特性是否可以做或模擬出m of n式的籤名？
A: 無法做到。組內有N把公鑰，則必須對應有N個籤名，缺一不可。每個人在生成籤名的時候，在哈希函數裏都代入的都是組公鑰P。

Q: 籤名機制的安全性如何衡量？
A: 主要取決於兩個：1. 籤名算法本身 2. 橢圓曲线。目前，Schnorr與ECDSA都用的是曲线secp256k1，這個層面一樣。至於籤名算法本身安全性，Schnorr目前有安全證明，安全優於ECDSA。

BCH上的

Schnorr籤名算法

早在2019年5月16日BCH已經开始進行硬分叉升級。升級的主要內容是Schnorr籤名算法和隔離見證復原，Schnorr籤名升級中最受期待的功能，而隔離見證復原則是一項修復性技術，用來找回被錯發到隔離見證地址的BCH。

开發人員Mark Lundeberg用戶不必生成新地址就可以开始使用Schnorr籤名。升級帶給BCH的優勢如下：

• 提高籤名數據的有效性：

  由於籤名是64字節的數據，與通常的70字節相比，交易可以減少4%的字節，該功能基本上提高了每筆比特幣現金交易所需的籤名數據的有效性（通過Schnorr籤名將使區塊鏈存儲和帶寬減少至少25％，使BCH網絡更快，更加高效）。並且升級後，Schnorr籤名給BCH帶來隱藏普通支付渠道的能力。

• 隱私性的提升：

  在升級之前很多用戶就會故意使用多個籤名來發送交易來提高隱私，而Schnorr籤名會使所有用戶的籤名看起來和任何其他籤名一樣，這種結構導致了交易隱私性的大幅提升。Schnorr提供的屬性以及BCH开發人員和基礎設施提供商（如錢包）添加的一些延展程序將進一步增強隱私和可擴展性。

• 對抗垃圾交易攻擊：

  在過去曾出現一種垃圾交易攻擊，攻擊者希望通過盡可能多的交易空間來使比特幣擁堵，他們的手段之一就是通過頻繁地從多個來源發送交易使這個交易中包括數十個籤名，這些籤名佔據了很多的空間，這是ECDSA籤名留下的隱患。

Schnorr可以規避這類的垃圾交易攻擊。如果每一筆交易只有一個籤名，那么區塊就能容納更多交易，垃圾交易制造者要想制造攻擊就必須發送更多交易，與更多人進行競爭，因此攻擊成本就會相對更高。籤名所佔空間通常是一筆交易最大的一部分，所以攻擊者不具優勢。

當然我們不能只看到好的一面，全則必缺,極則必反。尤其是量子計算機的發展對區塊鏈安全造成威脅，為了應對量子計算機對一些算法的攻擊，在2017年，NIST就开始了後量子密碼學標准化進程，其中由瑞士ABCMint數學算法基金會推動的抗量子籤名方案，後量子加密基金會支持的抗量子算法之一，最短籤名長度的籤名抗量子籤名方案——彩虹籤名Rainbow最被看好。

2017年8月，Jin Liu和數學家Prof. Jintai Ding籌建ABCMint，並注冊在瑞士蘇黎世附近的加密谷。其數字貨幣ABC底層籤名便是彩虹籤名Rainbow，他們愿景是在全球支持抗量子計算機破解算法的研究和應用，研究包括在全球支持數學家在算法方面的發現、破解、完善等，應用包括將合適的算法應用在主流數字加密貨幣方面。

他們認為比特幣從ECDSA改為Schnorr籤名的提案BIP340，採用Schnorr籤名，是比特幣的重大退步。不看好由計算機安全專家提出的算法選擇和改進，我們更偏重由數學家提出的算法選擇和改進，Schnorr籤名的問題很大，應該用在Litecoin之類先長時間試車。

BTC應等BCH，或其他鏈再用幾年Schnorr籤名再看看。Schnorr籤名最主要的優點是“多籤時籤名長度最短”，但缺點是“多籤時，最後一個人容易欺騙”。

在密碼學看來: 採用Schnorr籤名是一個"膽大不審慎”的做法，背離了”長期安全“的第一要義。

從密碼學角度看待Schnorr籤名主要是為了多籤名，而多籤名適合的場景應該是：既中心化又極其重要的場景，其極其重要的場景類似於核彈發射的十幾道Verifiable procedure。或夏延山核武基地之類的大門。而不應該是去中心化場景，或比特幣的發送這類場景。

簡單說：去中心化的，本身和多籤名是背離的。

下面來簡單科普一下幾種算法：

橢圓曲线數字

籤名算法（ECDSA）

橢圓曲线數字籤名算法（ECDSA，Elliptic Curve Digital Signature Algorithm）是使用橢圓曲线密碼（ECC）對數字籤名算法（DSA）的模擬（橢圓曲线密碼（ECC）由Neal Koblitz和Victor Miller於1985年發明），ECDSA首先由Scott和Vanstone在1992年為了響應NIST對數字籤名標准（DSS）的要求而提出。

比特幣目前使用的是 ECDSA 橢圓曲线數字籤名算法，要對消息 m 進行籤名，我們需對其進行哈希操作，並將此哈希視為一個數字：z = hash(m)。我們還需要一個隨機或隨機查找的數字 k。我們不喜歡信任隨機數生成器（存在太多的故障，很多漏洞與糟糕的 RGN 有關），因此，我們通常會使用RFC6979，並根據我們的祕密和我們要籤名的消息，計算確定性 K 值。

使用私鑰 pk，我們可以為包含兩個數字的消息 m 生成籤名：r （隨機點 R 的 x 坐標 = k×G） 和 s = (z+r⋅pk)/k。然後，使用我們的公鑰 P = pk×G，任何人都可通過檢查點 (z/s)×G+(r/s)×P 的 x 坐標等於 r，來驗證我們的籤名。

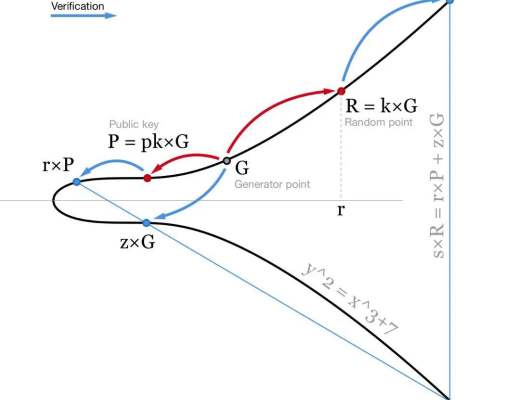
籤名驗證包括反轉（1/s）和兩點乘法，這些操作的計算量非常大。在比特幣中，每個節點都必須驗證所有交易。這意味着當你廣播一筆交易時，數千臺計算機將不得不驗證你的籤名。而簡化驗證過程將是非常有益的，即使籤名過程會更加困難。

第二，每個節點必須分別驗證每個籤名。如果是 m-of-n 多重籤名交易節點，則可能需多次驗證相同的籤名。例如，具有 7-of-11 多重籤名輸入的交易將包含 7 個籤名，並且需要對網絡中的每個節點進行 7-11 次的籤名驗證。同樣，這樣的交易會佔用大量的空間，你必須為此支付大量的費用。

Schnorr 籤名

Schnorr籤名算法是由德國數學家、密碼學家Claus Schnorr提出。並於1990年申請了專利，U.S. Patent 4,995,082，該專利與2008年2月失效。目前該算法可以自由使用。

Schnorr 籤名的生成則略有不同，我們使用了一個點 R 和一個標量 s 來代替兩個標量（r，s）。與 ECDSA 相似的是，R 是橢圓曲线（R=K×G）上的一個隨機點。籤名的第二部分計算略有不同 :

s = k + hash(P,R,m) ⋅ pk. 這裏的 pk 是你的私鑰，而 P = pk×G 則是你的公鑰，m 是消息。然後可通過檢查 s×G = R + hash(P,R,m)×P 來驗證這個籤名。

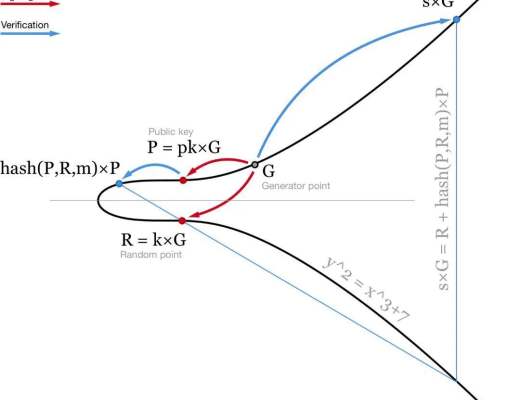
這個方程是线性的，所以方程可互相加減，並且仍然有效，這就給我們帶來了幾大關於 Schnorr 籤名的好處。

Schnorr 籤名的批量驗證

要驗證比特幣區塊鏈中的區塊，我們需確保區塊中的所有籤名都有效。

對於 ECDSA 籤名算法，每個籤名都必須單獨驗證。也就是說，如果區塊中有 1000 個籤名，我們就需要計算 1000 次倒置和 2000 次點乘運算，總共約 3000 次繁重的計算任務。

而通過使用 Schnorr 籤名，我們可以將所有籤名驗證方程相加，從而節省一些計算能力。對於有 1000 個籤名的區塊而言，我們需驗證：

(s1+s2+…+s1000)×G=(R1+…+R1000)+(hash(P1,R1,m1)×P1+hash(P2,R2,m2)×P2+…+hash(P1000,R1000,m1000)×P1000)

這裏我們有一堆加法（在計算能力上幾乎是免費的）以及 1001 次點乘法。我們需要為每個籤名計算大約一次繁重的計算。

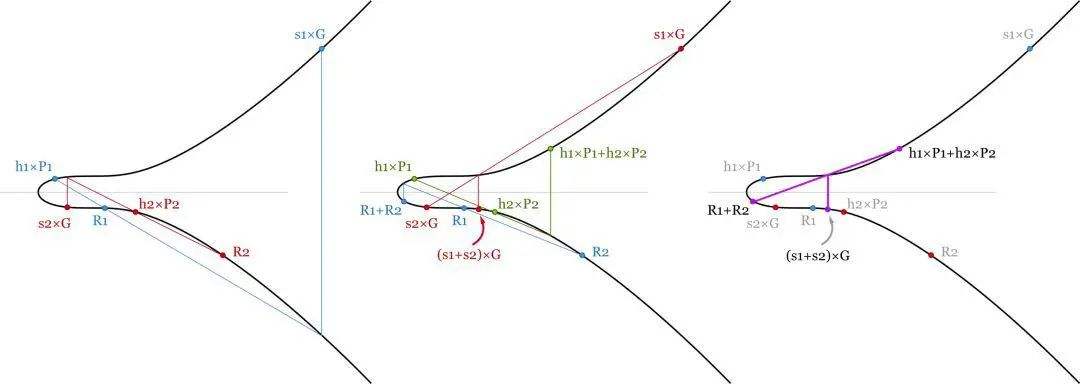
Schnorr 籤名的密鑰聚合

我們希望讓自己的比特幣保持安全，所以我們可能希望使用至少 2 個不同的私鑰來控制我們的比特幣。比如說一個放在筆記本電腦或手機，另一個則放在硬件錢包 / 冷錢包。因此，當其中一個受到威脅時，我們仍然可以控制我們的比特幣。

目前，它是通過 2-of-2 多重籤名腳本來實現的，這需要在交易中包含兩個單獨的籤名。而使用 schnorr 籤名，我們可以使用一對私鑰(pk1,pk2)，並生成一個與共享公鑰 P=P1+P2=pk1×G+pk2×G 對應的共享籤名。要生成這個籤名，我們需要在每個設備上選擇一個隨機數（k1，k2），生成一個隨機點 Ri=ki×G，將它們相加以計算一個公共哈希 (P,R1+R2,m)，然後從每個設備 (si = ki + hash(P,R,m) ⋅ pki) 中獲取 s1 和 s2。然後我們可以將這些籤名相加，並使用一對 (R, s) = (R1+R2, s1+s2) 作為我們對共享公鑰 p 的籤名。其他所有人都無法說出它是否是聚合籤名，它看起來與普通 schnorr 籤名完全相同。

這種構造有 3 個問題，第一，從用戶界面的角度來看，要進行交易，我們需要進行幾輪通信，計算公共 R，然後-籤名。有了兩個私鑰，只需一次訪問冷錢包就可以完成：我們在在线錢包上准備一個未籤名的交易，選擇 k1，將 R1=K1×G 與未籤名的交易一起記下。然後我們將這些數據傳送到冷錢包並籤名。因為我們已經有了 R1，所以我們可以一次性在冷錢包上籤署交易。從冷錢包中，我們得到了 R2 和 s2，並將其傳輸回在线錢包。在线錢包使用之前選擇的 (k1, R1) 籤署交易，結合籤名並廣播籤名交易。這與我們現在的情況非常相似，但一旦添加第三個私鑰，一切就會變得更加復雜。比方說，你有一筆財富，它是由 10 個私鑰控制的，它們存儲在世界各地不同的安全位置，然後，你需要進行一筆交易。目前，你只需要瀏覽所有這些位置一次，但如果你使用的是密鑰聚合，則需要執行兩次，以組裝所有 RI，然後籤名。在這種情況下，最好在不進行聚合的情況下保留單獨的籤名，然後我們就需要 3 輪通信：

1. 選擇一個隨機數 ki 和相應的 Ri=ki×G，然後只告訴每個人其哈希 ti=hash(Ri)，這樣每個人都可以確定在學習了其他隨機數之後你不會改變主意；

2. 把所有的數字匯總起來，計算出共同的 R；

3. 籤名；

第二個問題是已知的惡意密鑰攻擊。無論是在論文還是這篇文章中，都有很好的描述，所以我不想詳細討論。其想法是，如果你的某個設備被黑客攻擊（比如說，你的在线錢包），並假裝其公鑰是 （p1-p2），那么它可以用它的私鑰 pk1 控制共享資金。一個簡單的解決方案是，在設置設備時，需要使用相應的私鑰對公鑰進行籤名。

還有第三個重要問題。不能使用確定性 k 進行籤名。有一種簡單的攻擊方式，如果你使用確定性 K，它允許黑客獲得我們的私鑰。攻擊看起來會是這樣的：有人入侵了我們的筆記本電腦，並完全控制了兩個私鑰中的一個（例如 pk1）。我們可能覺得是安全的，因為我們的比特幣需要來自 pk1 和 pk2 的聚合籤名。因此，我們嘗試像往常一樣進行交易，准備一個未籤名的交易和 R1 值，將它們轉移到我們的硬件錢包並在那裏籤名。然後返回 （r2，s2） 和……我們的在线錢包發生了一些事情，它無法籤名和廣播。我們再次嘗試，但我們被黑的電腦這次使用了另一個隨機值 R1'。我們再次與我們的硬件錢包籤署相同的交易，並將值 （r2，s2） 帶回我們被黑的電腦。然後，糟糕的事就發生了，我們的比特幣就丟失了。

在這個攻擊中，黑客為同一筆交易獲得一對有效的籤名：(R1, s1, R2, s2) 和 (R1', s1', R2, s2')，這裏 R2 是相同的，但 R = R1+R2 和 R'=R1'+R2 是不同的，這意味着黑客可以計算我們的第二個私鑰：s2-s2'=(hash(P,R1+R2,m)-hash(P,R1'+R2,m))⋅pk2 and pk2=(s2-s2')/(hash(P,R1+R2,m)-hash(P,R1'+R2,m))。我發現這是密鑰聚合最不方便的特性：我們需要在任何地方使用好的隨機數生成器來使用密鑰聚合。

彩虹籤名

Rainbow是一種多變量籤名方案，它的分層結構以不平衡石油-醋慄（UOV）籤名方案為基礎。Rainbow層所施加的額外結構使該方案面臨更多的密碼分析技術，但提高了該方案的效率。Rainbow提供了快速的籤名和驗證以及非常短的籤名，但具有非常大的公鑰。

選擇Rainbow增加了入圍籤名方案的多樣性；但是，由於密鑰尺寸非常大，Rainbow不適合作為通用籤名算法來替代目前出現在FIPS 186-4中的算法。特別是，大公鑰使得證書鏈非常大。然而，有些應用並不需要經常發送密鑰。對於這樣的應用，Rainbow提供了小而快的籤名。

參考文獻：

https://panzhibiao.com/2019/02/28/schnorr-sigature/

https://mp.weixin.qq.com/s/wy1jtKzNVdmiccd4e9N3Ew

https://medium.com/cryptoadvance/bls-signatures-better-than-schnorr-5a7fe30ea716https://medium.com/cryptoadvance/how-schnorr-signatures-may-improve-bitcoin-91655bcb4744

鄭重聲明：本文版權歸原作者所有，轉載文章僅為傳播信息之目的，不構成任何投資建議，如有侵權行為，請第一時間聯絡我們修改或刪除，多謝。