LUCIDA：如何利用多因子策略構建強大的加密資產投資組合（數據預處理篇）

2023-11-28 08:11:05

前言

書接上回，我們發布了《用多因子策略構建強大的加密資產投資組合》系列文章的第一篇 - 理論基礎篇，本篇是第二篇 - 數據預處理篇。

在計算因子數據前/後，以及測試單因子的有效性之前，都需要對相關數據進行處理。具體的數據預處理涉及重復值、異常值/缺失值/極端值、標准化和數據頻率的處理。

一、重復值

數據相關定義：

鍵（ Key ）：表示一個獨一無二的索引。eg. 對於一份有全部 token 所有日期的數據，鍵是“token_id/contract_address - 日期”
值（Value）：被鍵索引的對象就稱之為“值”。

診斷重復值的首先需要理解數據“應當”是什么樣子。通常數據的形式有：

時間序列數據（Time Series）。鍵是“時間”。eg.單個 token 5 年的價格數據
橫截面數據（Cross Section)。鍵是“個體”。eg.2023.11.01 當日 crypto 市場所有 token 的價格數據
面板數據（Panel）。鍵是“個體-時間”的組合。eg.從 2019.01.01-2023.11.01 四年所有 token 的價格數據。

原則：確定了數據的索引（鍵），就能知道數據應該在什么層面沒有重復值。

檢查方式：

pd.DataFrame.duplicated(subset=[key 1, key 2, ...])

檢查重復值的數量：pd.DataFrame.duplicated(subset=[key 1, key 2, ...]).sum()
抽樣看重復的樣本：df[df.duplicated(subset=[...])].sample()找到樣本後，再用 df.loc 選出該索引對應的全部重復樣本

pd.merge(df 1, df 2, on=[key 1, key 2, ...], indicator=True, validate='1: 1')

在橫向合並的函數中，加入 indicator 參數，會生成_merge 字段，對其使用 dfm['_merge'].value_counts()可以檢查合並後不同來源的樣本數量
加入 validate 參數，可以檢驗合並的數據集中索引是否如預期一般（1 to 1、 1 to many 或 many to many，其中最後一種情況其實等於不需要驗證）。如果與預期不符，合並過程會報錯並中止執行。

二、異常值/缺失值/極端值

產生異常值的常見原因：

極端情況。 比如 token 價格 0.000001 $或市值僅 50 萬美元的 token，隨便變動一點，就會有數十倍的回報率。
數據特性。 比如 token 價格數據從 2020 年 1 月 1 日开始下載，那么自然無法計算出 2020 年 1 月 1 日的回報率數據，因為沒有前一日的收盤價。
數據錯誤。 數據提供商難免會犯錯，比如將 12 元每 token 記錄成 1.2 元每 token。

針對異常值和缺失值處理原則：

刪除。對於無法合理更正或修正的異常值，可以考慮刪除。
替換。通常用於對極端值的處理，比如縮尾（Winsorizing）或取對數（不常用）。
填充。對於 缺失值 也可以考慮以合理的方式填充，常見的方式包括均值（或移動平均）、插值（Interpolation）、 填 0 df.fillna( 0)、向前 df.fillna('ffill')/向後填充 df.fillna('bfill')等，要考慮填充所依賴的假設是否合。

機器學習慎用向後填充，有 Look-ahead bias 的風險

針對極端值的處理方法：

1.百分位法。

通過將順序從小到大排列，將超過最小和最大比例的數據替換為臨界的數據。對於歷史數據較豐富的數據，該方法相對粗略，不太適用，強行刪除固定比例的數據可能造成一定比例的損失。

2. 3σ / 三倍標准差法

對數據範圍內的所有因子做出如下調整：

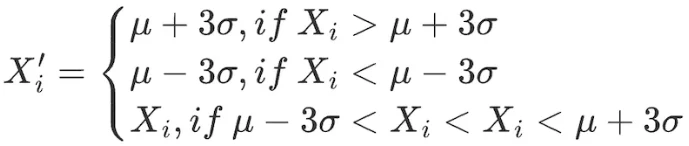
該方法不足在於，量化領域常用的數據如股票價格、token 價格常呈現尖峯厚尾分布，並不符合正態分布的假設，在該情況下採用 3 σ方法將有大量數據錯誤地被識別為異常值。

3.絕對值差中位數法（Median Absolute Deviation, MAD）

該方法基於中位數和絕對偏差，使處理後的數據對極端值或異常值沒那么敏感。比基於均值和標准差的方法更穩健。

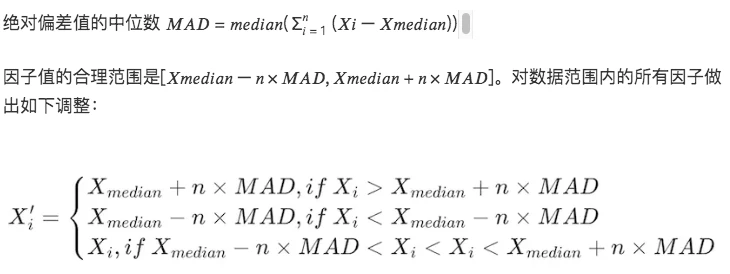
# 處理因子數據極端值情況

class Extreme(object):
def __init__(s, ini_data):
s.ini_data = ini_data

def three_sigma(s, n= 3):
mean = s.ini_data.mean()
std = s.ini_data.std()
low = mean - n*std
high = mean + n*std

return np.clip(s.ini_data, low, high)

def mad(s, n= 3):
median = s.ini_data.median()
mad_median = abs(s.ini_data - median).median()
high = median + n * mad_median
low = median - n * mad_median

return np.clip(s.ini_data, low, high)

def quantile(s, l = 0.025, h = 0.975):
low = s.ini_data.quantile(l)
high = s.ini_data.quantile(h)
return np.clip(s.ini_data, low, high)

三、標准化

1.Z-score 標准化

2.最大最小值差標准化（Min-Max Scaling）

將每個因子數據轉化為在( 0, 1) 區間的數據，以便比較不同規模或範圍的數據，但它並不改變數據內部的分布，也不會使總和變為 1 。

由於考慮極大極小值，對異常值敏感
統一量綱，利於比較不同維度的數據。

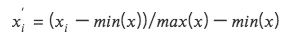
3.排序百分位（Rank Scaling）

將數據特徵轉換為它們的排名，並將這些排名轉換為介於 0 和 1 之間的分數，通常是它們在數據集中的百分位數。*

由於排名不受異常值影響，該方法對異常值不敏感。
不保持數據中各點之間的絕對距離，而是轉換為相對排名。

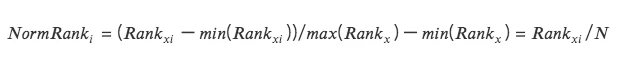
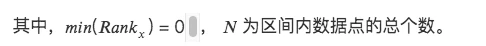
# 標准化因子數據 class Scale(object):
def __init__(s, ini_data, date):
s.ini_data = ini_data
s.date = date
def zscore(s):
mean = s.ini_data.mean()
std = s.ini_data.std()
return s.ini_data.sub(mean).div(std)
def maxmin(s):
min = s.ini_data.min()
max = s.ini_data.max()
return s.ini_data.sub(min).div(max - min)
def normRank(s):
# 對指定列進行排名，method='min'意味着相同值會有相同的排名，而不是平均排名
ranks = s.ini_data.rank(method='min')
return ranks.div(ranks.max())