HOKIE: Introduces the Plookup algorithm

The basic idea

The problem Plookup tries to solve is to prove, given two sets, that elements of one set are in the other. Given two sets t and f, s is the sorted result of f. If the element in T appears at least once in F. To determine whether an element in F is included in T, we only need to compare the set of element differences:

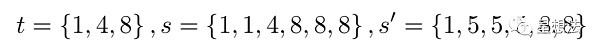
For example, t is the set {1,4,8}, and the difference set of elements is {3, 4}, which are 4-1, 8-4 respectively. If s consists only of elements in t and each element occurs at least once, such as {1,1,4,8,8,8}, the set of differences of elements is also {3,4}. If the elements in S are not exactly elements in T, it does not follow that the elements in S are in the set of T even if the set of element differences is the same. For example, s is {1, 5,5, 5, 8, 8}, and the difference set of elements is {3,4}, 8-5, 5-1, respectively.

A random factor can be introduced to determine the dependency of two sets by adding the preceding and following elements.

Defining polynomial

On the basis of the basic idea, two polynomials F and G are defined:

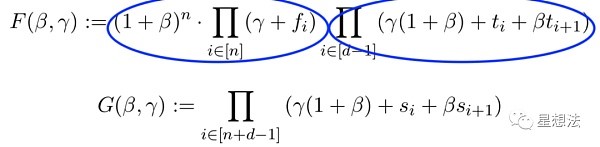
If F and G are equivalent to each other, the following conditions are true:

• F is a member of t

• s is the union of (f, t) and is ordered by the elements in t

If this is true, it follows that the two polynomials are equal. F polynomials can be viewed as having two parts, two serial products. You can view this as a multiplication of the elements in t. You can view this as a multiplication of the elements of f. Since the elements in F belong to t, the multiplication of the elements in F can be imagined as a multiplication of the same elements. Conversely, because of the random factors of beta and gamma, the two conditions satisfied can also be deduced from the F and G equivalents.

On the basis of defining polynomials, the problem can be transformed into two polynomials equal.

Plookup agreement

If you know f and t, you can sort it to get s. Since S is a combination of f and t, s can be represented by two functions, h1 and h2. The key is step 4, which defines the Z function:

• Z(g) = 1 - I started with 1

• Z(x) is the quotient of two polynomials

• Z(g^(n+1)) = 1 - n+1, both polynomials are equal

The verifier, in addition to looking at the Z function, also looks at the H1 / H2 continuity.

conclusion

Plookup proposes a protocol for proving the correctness of a function operation in the case of explicit input/output. The input and output are defined as lookup tables. The calculated input/result is correct as long as it is in the lookup table. Plookup and Plonk adopt the same idea, Plookup defines the polynomial representation of the problem, and proves the recursive representation and boundary of the Z function.

鄭重聲明：本文版權歸原作者所有，轉載文章僅為傳播信息之目的，不構成任何投資建議，如有侵權行為，請第一時間聯絡我們修改或刪除，多謝。