BIP 158 致密區塊過濾器詳解

2023-07-01 00:07:48

作者：Elle Mouton

在本文中，我會簡要介紹比特幣輕客戶端的需要，以及為什么 “致密區塊過濾器（compact block filters）” 比 “布隆過濾器（Bloom filters）” 更好地滿足了這種需要。然後，我會深入解釋致密區塊過濾器是怎么工作的，並會附上在測試網上構造這樣的過濾器的逐步講解。

區塊過濾器的意義

比特幣輕客戶端（bitcoin light software）是一種軟件，其目標是不存儲比特幣區塊鏈但支持比特幣錢包。這意味着，它需要能夠向網絡廣播交易，但最重要的是，它必須能夠從鏈上找出跟本錢包相關的新交易。這樣的相關交易有兩種：給本錢包發送資金（為本錢包的一個地址創建了一個新的輸出）、花費本錢包所控制的其中一個 UTXO。

布隆過濾器有什么問題？

在 BIP 158 出現以前，輕客戶端最常用的方法是由 BIP 37 描述的布隆過濾器 1。布隆過濾器的模式是，你找出自己感興趣的所有數據對象（比如，被花費的以及被創建的 UTXO 的腳本公鑰）、將它們逐個多次哈希，然後將每個結果添加到一個叫做 “布隆過濾器” 的位圖（bit map）中。這個過濾器代表了你感興趣的東西。然後，你將這個過濾器發送給一個你信任的比特幣節點，並要求他們給你發送所有跟這個過濾器相匹配的東西。

問題在於，這個過程並不是非常私密，因為，你還是向這個接收過濾器的比特幣節點泄露了一些信息。他們可以知曉你感興趣的交易以及你完全沒興趣的交易；他們還可以不給你發送跟過濾器相匹配的東西。所以，這對輕客戶端來說並不是理想的。但同時，它對向輕客戶端提供服務的比特幣節點來說也不理想。每次你發送一個過濾器，他們就必須從硬盤加載相關的區塊，然後確定是否有交易跟你的過濾器相匹配。只需要不停發送假的過濾器，你就可以轟炸他們 —— 這本質上是一種 DOS 攻擊。只需要非常少的能量就可以創建一個過濾器，但需要耗費很多能量，才能響應這樣的請求。

致密區塊過濾器

OK，那么我們需要的屬性有：

更強的隱私性
客戶端-服務端的負載更少不對稱性。即，服務端需要做的工作應該更少。
更少信任。輕客戶端不需要擔心服務端不返回相關的交易。

使用致密區塊過濾器，服務端（全節點）將為每個區塊構造一個確定性的過濾器，包含這個區塊中的所有數據對象。這個過濾器只需計算一次，就可以永久保存下來。如果輕客戶端請求某一個區塊的過濾器，這裏是沒有不對稱性的 —— 因為服務端不需要做比發起請求的客戶端更多的工作。輕客戶端也可以選擇多個信息源來下載完整的區塊，以確保它們是一致的；而且，輕客戶端總是可以下載完整的區塊，從而自己檢查服務端所提供的過濾器是不是正確的（與相關的區塊內容相匹配）。另一個好處是，這種方式更加隱私。輕客戶端不再需要給服務端發送自己想要的數據的指紋。這樣分析一個輕客戶端的活動也會變得更加困難。輕客戶端從服務端獲取這樣的過濾器之後，自己檢查過濾器中是否有自己想要的數據，如果有，輕客戶端就請求完整的區塊。還要指出的一點是，為了以這種方式服務輕客戶端，全節點需要持久保存這些過濾器，而輕客戶端可能也想要持久保存少數幾個過濾器，所以，保證過濾器盡可能輕量，是非常重要的（這也是為什么它叫做 “致密區塊過濾器”）。

很好！現在我們要進入難得東西了。這樣的過濾器是怎么創建的？它看起來是什么樣子的？

我們的需求是？

我們想把特定對象的指紋放在過濾器中，這樣一來，當客戶端想要檢查一個區塊是否可能包含了跟自己相關的內容時，他們可以列舉所有的對象，並檢查一個過濾器是否與這些對象匹配。
我們希望這個過濾器盡可能小。
實質上，我們想要的是某種東西，它可以用一個遠遠小於區塊的體積，來總結一個區塊的某一些信息。

包含在過濾器中的基本信息有：每一筆交易的輸入的腳本公鑰（也就是每一個被花費的 UTXO 的腳本公鑰），以及每一筆交易的每一個輸出的腳本公鑰。基本上就是這樣：

objects = {spk1, spk2, spk3, spk4, ..., spkN} // 一個由 N 個腳本公鑰構成的列表

從技術上來說，我們到這裏就可以止步了 —— 就這樣的腳本公鑰列表，也可以充當我們的過濾器。這是一個區塊的濃縮版本，包含了輕客戶端所需的信息。有了這樣的列表，輕客戶端可以 100% 確認一個區塊中是否有自己感興趣的交易。但這樣的列表體積非常大。所以，我們接下來的步驟，都是為了讓這個列表盡可能緊湊。這就是讓事情有趣起來的地方。

首先，我們可以將每一個對象都轉化成某個範圍內的一個數字、並使得每個對象數字在這個範圍內是均勻分布的。假設我們有 10 個對象（N = 10），然後我們有某一種函數，可以將每個對象都轉化成一個數字。假設我們選擇的範圍是 [0, 10]（因為我們有 10 個對象）。現在，我們的 “哈希加轉換成數字” 函數將取每一個對象為輸入，並分別產生一個大小在 [0, 10] 之間的數字。這些數字在這個範圍內是均勻分布的。這就意味着，在排序之後，我們將得到一個這樣的圖（在非常非常理想的情況下）：

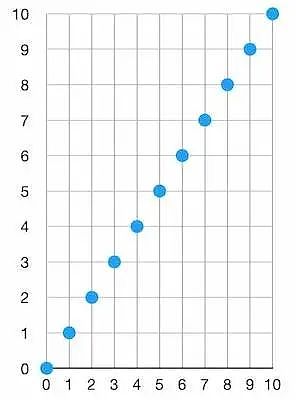
首先，這非常棒，因為我們已經大大縮減了每一個對象的指紋的大小。現在每個對象都只是一個數字了。那么，我們的新過濾器看起來就像這樣：

numbers := {1,2,3,4,5,6,7,8,9,10}

輕客戶端下載這樣的過濾器，希望知道自己正在尋找的某個對象是否跟這個過濾器相匹配。他們只需取出自己感興趣的對象，然後運行相同的 “哈希加轉換成數字” 函數，看看結果是否在這個過濾器中，就可以了。問題在哪裏呢？問題是過濾器中的數字已經佔據了這個空間內的一切可能性！這意味着，不管輕客戶端關心什么樣的對象，產生的數字結果都一定會跟這個過濾器相匹配。換句話來說，這個過濾器的 “假陽性率（false-positive rate）” 為 1 （譯者注：這裏的 “假陽性” 指區塊中可能不包含客戶端所關心的交易，但通過過濾器得到的結果卻是有）。這就不太好了。這也說明，在我們壓縮數據以生成過濾器的過程中，我們弄丟了太多信息。我們需要更高的假陽性率。那么，假設我們希望假陽性率為 5.那么，我們可以讓區塊內的對象均勻匹配到 [0, 50] 範圍內的數字：

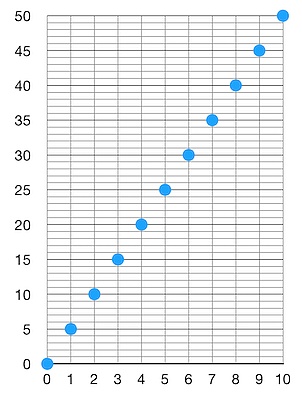
這樣看起來就好一些了。如果我是一個客戶端，下載到了這樣的過濾器，要通過過濾器檢查一個我關心的對象是否在對應的區塊中，過濾器說有但區塊中並沒有（假陽性）的概率就下降到 1/5 。很好，現在我們是將 10 個對象映射成了 0 到 50 之間的數字。這個新的數字列表就是我們的過濾器。再說一遍，我們隨時可以停下來，但是，我們也可以進一步壓縮它們！

現在，我們有了一個有序的數字列表，這些數字均勻地分布在 [0, 50] 區間內。我們知道這個列表中有 10 個數字。這意味着，我們可以推斷出，在這個有序數字列表內，相鄰兩個數字的差值最有可能是 5 。總的來說，如果我們有 N 個對象，並希望假陽性率為 M，那么空間的大小應該是 N * M 。也即這些數字的大小應該在 0 到 N * M 之間，但（排序之後）相鄰兩個數字檢查的插值大概率是 M 。而 M 存儲起來肯定比 N * M 空間內的數字要小。所以，我們不必存儲每一個數字，我們可以存儲相鄰兩個數字的差值。在上面這個例子中，這意味着，我們不是存儲 [0, 5, 10, 15, 20, 25, 30, 35, 40, 45, 50] 作為過濾器，而是存儲 [0, 5, 5, 5, 5, 5, 5, 5, 5, 5]，憑此重構初始列表是很簡單的。如你縮減，存儲數字 50，顯然比存儲數字 5 要佔用更多空間。但是，為何要止步呢？我們再壓縮多一點！

接下來就要用到 “Golomb-Rice 編碼” 了。這種編碼方式可以很好地編碼一個表內各數字都非常接近與某一個數字的列表。而我們的列表恰好就是這樣的！我們的列表中的數字，每一個都很可能接近 5（或者說，接近於我們的假陽性率，即 M），所以，取每一個數字與 M 的商（將每一個數字除以 5 並忽略掉余數），將很有可能是 0 （如果數字稍小於 5）或者 1（數字稍大於 5）。商也有可能是 2、3，等等，但概率會小很多。很棒！所以我們可以利用這一點：我們將用盡可能少的比特來編碼更小的商，同時使用更多的比特幣來編碼更大、但更不可能出現的商。然後，我們還需要編碼余數（因為我們希望能夠准確地重建整個列表），而這些余數總是在 [0, M - 1] 範圍內（在這個案例中就是 [0, 4]）。為編碼商，我們使用下列映射：

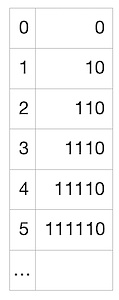
上述映射很容易理解：數字 1 的數量表示了我們要編碼的商，而 0 表示商編碼的結尾。所以，對我們列表中的每一個數字，我們都可以使用上述表格來編碼商，然後使用可以表示最大值為 M-1 的比特川，將余數轉化為 2 進制。在這裏余數為 4，只需要 3 個比特就可以了。這裏是一個展示我們的例子中可能的余數及其編碼的表格：

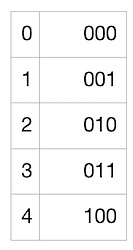
所以，在理想的情況下，我們的列表 [0, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5] 可以編碼成：

0000 10000 10000 10000 10000 10000 10000 10000 10000 10000

在我們轉移到一個更現實的案例之前，我們來看看是否可以靠這個過濾器恢復我們的最初的列表。

現在我們擁有的是 “0000100001000010000100001000010000100001000010000”。我們知道 Golomb-Rice 編碼，也知道 M 為 5（因為這將是公开知識，每一個使用這種過濾器構造的人都會知曉）。因為我們知道 M 為 5，所以我們知道會有 3 個比特來編碼余數。所以，我們可以將這個過濾器轉化成下列的 “商-余數” 數組列表：

[(0, 0), (1, 0), (1, 0), (1, 0), (1, 0), (1, 0), (1, 0), (1, 0), (1, 0), (1, 0)]

知道商是通過除以 M（5）得到的，所以我們可以恢復出：

[0, 5, 5, 5, 5, 5, 5, 5, 5, 5]

而且，我們知道這個列表所表示的是相鄰兩數之間的差值，所以我們可以恢復最初的列表：

[0, 5, 10, 15, 20, 25, 30, 35, 40, 45, 50]

更加現實的例子

我們現在要嘗試為一個真實的比特幣 testnet 區塊構造一個過濾器。我將使用區塊 2101914 。我們看看它的過濾器長什么樣：

$ bitcoin-cli getblockhash 2101914
000000000000002c06f9afaf2b2b066d4f814ff60cfbc4df55840975a00e035c

$ bitcoin-cli getblockfilter 000000000000002c06f9afaf2b2b066d4f814ff60cfbc4df55840975a00e035c
{
  "filter": "5571d126b85aa79c9de56d55995aa292de0484b830680a735793a8c2260113148421279906f800c3b8c94ff37681fb1fd230482518c52df57437864023833f2f801639692646ddcd7976ae4f2e2a1ef58c79b3aed6a705415255e362581692831374a5e5e70d5501cdc0a52095206a15cd2eb98ac980c22466e6945a65a5b0b0c5b32aa1e0cda2545da2c4345e049b614fcad80b9dc9c903788163822f4361bbb8755b79c276b1cf7952148de1e5ee0a92f6d70c4f522aa6877558f62b34b56ade12fa2e61023abf3e570937bf379722bc1b0dc06ffa1c5835bb651b9346a270",
  "header": "8d0cd8353342930209ac7027be150e679bbc7c65cc62bb8392968e43a6ea3bfe"
}

好了親愛的，看看我們如何從區塊構造出這樣的過濾器吧。

這裏所用的完整代碼可以在這個 github 庫中找到。我在這裏只會展示一些僞代碼片段。這段代碼的核心是一個名為 constructFilter 的函數，比特幣客戶端可以用它來調用 bitcoind 以及對應的區塊。這個函數看起來是這樣的：

func constructFilter(bc *`bitcoind`.Bitcoind, block `bitcoind`.Block) ([]byte, error) {
    // 1. 從區塊中收集我們想要添加到一個過濾器中的所有對象

    // 2. 將這些對象轉化為數字，並排序 

    // 3. 取得排序後的數字列表中相鄰兩數的差值

    // 4. 使用 Golomb-Rice 編碼來編碼這些差值
}

所以，第一步是從區塊中收集我們想要添加到過濾器中的所有對象。從 BIP 出發，我們知道，這些對象包括所有被花費的腳本公鑰，以及每一個輸出的腳本公鑰。BIP 還設定了一些額外的規則：我們會跳過 coinbase 交易的輸入（因為它沒有輸入，這是沒有意義的），而且我們會通過所有 OP_RETURN 輸出。我們也會刪除重復數據。如果有兩個相同的腳本公鑰，我們只會向過濾器添加一次。

// 我們希望向過濾器添加的對象的列表
// 包括所有被花費的腳本公鑰，以及每一個輸出的腳本公鑰
// 我們使用了 “圖（map）”，這樣就去除了重復的腳本公鑰
objects := make(map[string] struct{})

// 便利區塊中的每一筆交易
for i, tx := range block.Tx {

        // 添加每一個輸出的腳本公鑰
        // 到我們的對象列表中
        for _, txOut := range tx.Vout {
                scriptPubKey := txOut.ScriptPubKey

                if len(scriptPubKey) == 0 {
                        continue
                }

                // 如遇 OP_RETURN (0x6a) 輸出，則跳過
                if spk[0] == 0x6a {
                        continue
                }

                objects[skpStr] = struct{}{}
        }

        // 不添加 coinbase 交易的輸入
        if i == 0 {
                continue
        }

        // 對每一個輸入，獲取其腳本公鑰
        for _, txIn := range tx.Vin {
                prevTx, err := bc.GetRawTransaction(txIn.Txid)
                if err != nil {
                        return nil, err
                }

                scriptPubKey := prevTx.Vout[txIn.Vout].ScriptPubKey

                if len(scriptPubKey) == 0 {
                        continue
                }

                objects[spkStr] = struct{}{}
        }
}

OK，現在已經收集好了所有的對象。現在，我們定義變量 N 為對象圖的長度。在這裏，N 為 85 .

下一步則是將我們的對象轉換成在一個區間內均勻分布的數字。再說一次，這個範圍取決於你想要多高的假陽性率。BIP158 定義常量 M 為 784931 。這意味着，出現假陽性的概率為 1/784931 。就像我們前面做的一樣，我們取假陽性率 M 乘以 N，得到所有數字的分布範圍。這個範圍我們定義為 F，即 F = M * N 。在這裏，F = 66719135 。我不准備細說將對象映射為數字的函數（你可以在上面鏈接的 github 庫中找到相關的細節）。你需要知道的僅僅是，它會取對象、常量 F（定義了需要將對象映射到的範圍）以及一個鍵（區塊哈希值）作為輸入。一旦我們得出所有的數字，我們會用升序排列這個列表，然後創建一個叫做 differences（差值）的新列表，保存排好序的數字列表內相鄰兩個數字之間的差值。

numbers := make([]uint64, 0, N)

// 遍歷所有對象，將它們轉化為在 [0, F] 範圍內均勻分布的數字
// 並將這些數字存儲為 `numbers` 列表
for o := range objects {
        // Using the given key, max number (F) and object bytes (o),
        // convert the object to a number between 0 and F.
        v := convertToNumber(b, F, key)

        numbers = append(numbers, v)
}

// 給 numbers 列表排序
sort.Slice(numbers, func(i, j int) bool { return numbers[i] < numbers[j] })

// 將數字列表轉化為差值列表
differences := make([]uint64, N)
for i, num := range numbers {
        if i == 0 {
                differences[i] = num
                continue
        }

        differences[i] = num - numbers[i-1]
}

很棒！這裏有張圖，展示了 numbers 和 differences 列表。

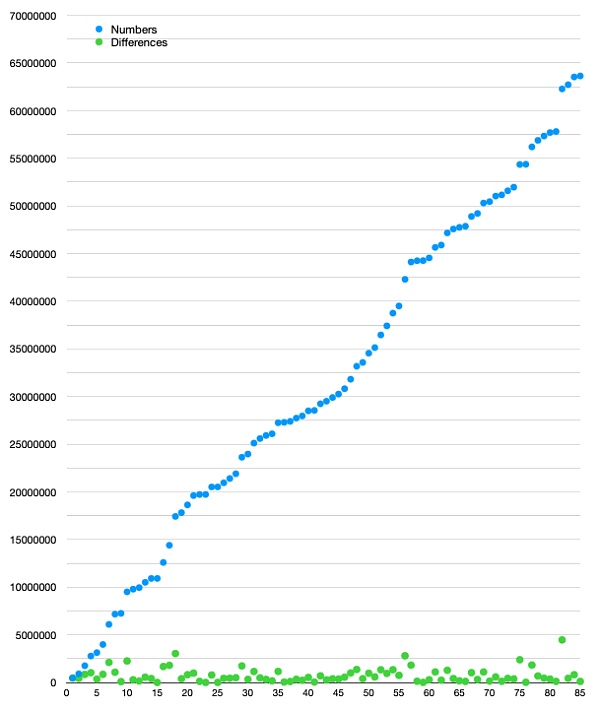
如你縮減，85 個數字均勻地分布在整個空間中！所以 differences 列表中的數值也非常小。

最後一步是用 Golomb-Rice 編碼來編碼這個 differences 列表。回憶一下前面的解釋，我們需要用最有可能的數值來除每個差值，然後編碼商和余數。在我們前面的例子中，我說最有可能的數值就是 M，而余數會在 [0, M] 之間。但是，BIP158 並不是這么做的，因為我們發現 2，這並不是事實上能讓最終的過濾器體積最小化的參數。所以我們不使用 M，而是定義一個新的常量 P，並使用 2 ^ P 作為 Golomb-Rice 參數。P 定義成 19 。這意味着我們要將每一個差值除以 2 ^ 19，以獲得商和余數，並且余數會用 19 比特編碼成二進制。

filter := bstream.NewBStreamWriter(0)

// 對於 `differences` 列表中的每個數值，通過除以 2 ^ P 來獲得商和余數。
for _, d := range differences {
        q := math.Floor(float64(d)/math.Exp2(float64(P)))
        r := d - uint64(math.Exp2(float64(P))*q)

        // 編碼商
        for i := 0; i < int(q); i++ {
               filter.WriteBit(true)
        }
        filter.WriteBit(false)

        filter.WriteBits(r, P)
}

很棒！現在我們可以輸出過濾器了，得到：

71d126b85aa79c9de56d55995aa292de0484b830680a735793a8c2260113148421279906f800c3b8c94ff37681fb1fd230482518c52df57437864023833f2f801639692646ddcd7976ae4f2e2a1ef58c79b3aed6a705415255e362581692831374a5e5e70d5501cdc0a52095206a15cd2eb98ac980c22466e6945a65a5b0b0c5b32aa1e0cda2545da2c4345e049b614fcad80b9dc9c903788163822f4361bbb8755b79c276b1cf7952148de1e5ee0a92f6d70c4f522aa6877558f62b34b56ade12fa2e61023abf3e570937bf379722bc1b0dc06ffa1c5835bb651b9346a270

除了开頭的兩個字節，其余都跟我們在 bitcoind 中得到的過濾器完全一樣！為什么前面的 2 字節會有區別呢？因為 BIP 說 N 的值需要在 CompactSize 格式中編碼，並出現在過濾器的前面，這樣才能被接收者解碼。這是用下列辦法完成的：

fd := filter.Bytes()

var buffer bytes.Buffer
buffer.Grow(wire.VarIntSerializeSize(uint64(N)) + len(fd))

err = wire.WriteVarInt(&buffer, 0, uint64(N))
if err != nil {
        return nil, err
}

_, err = buffer.Write(fd)
if err != nil {
        return nil, err
}

如果我們現在再打印出過濾器，就會發現它跟 bitcoind 的結果完全一樣：

5571d126b85aa79c9de56d55995aa292de0484b830680a735793a8c2260113148421279906f800c3b8c94ff37681fb1fd230482518c52df57437864023833f2f801639692646ddcd7976ae4f2e2a1ef58c79b3aed6a705415255e362581692831374a5e5e70d5501cdc0a52095206a15cd2eb98ac980c22466e6945a65a5b0b0c5b32aa1e0cda2545da2c4345e049b614fcad80b9dc9c903788163822f4361bbb8755b79c276b1cf7952148de1e5ee0a92f6d70c4f522aa6877558f62b34b56ade12fa2e61023abf3e570937bf379722bc1b0dc06ffa1c5835bb651b9346a270

成功！

不過，我個人的理解是，不需要把 N 加入過濾器中。如果你知道 P 的值，那你就能找出 N 的值。來看看我們是否能用第一個過濾器輸出恢復初始的數字列表：

b := bstream.NewBStreamReader(filter)
var (
    numbers []uint64
    prevNum uint64
)

for {

        // 從字節串中讀取商。遇到的第一個 0 表示商的結尾
        // 再遇到 0 之前，1 的數量就代表了商
        var q uint64
        c, err := b.ReadBit()
        if err != nil {
                return err
        }

        for c {
                q++
                c, err = b.ReadBit()
                if errors.Is(err, io.EOF) {
                        break
                } else if err != nil {
                        return err
                }
        }

        // 隨後的 P 個比特編碼了余數
        r, err := b.ReadBits(P)
        if errors.Is(err, io.EOF) {
                break
        } else if err != nil {
                return err
        }

        n := q*uint64(math.Exp2(float64(P))) + r

        num :=  n + prevNum
        numbers = append(numbers, num)
        prevNum = num
}

fmt.Println(numbers)