一種安全的 LP 價格的獲取方法

前言

目前，使用 LP Token 進行抵押借貸的需求越來越大，但是目前市面上並沒有一種完善的用於安全獲取 LP Token 價格的方法。慢霧安全團隊在分析 LP Token 價格的獲取方式的過程中關注到了 Alpha Finance 團隊的關於安全獲取 LP 價格的方法。在仔細閱讀後，將相關的思考分享給大家。

LP Token 價格獲取分析

目前，常見的 LP Token 價格的獲取方式如下：

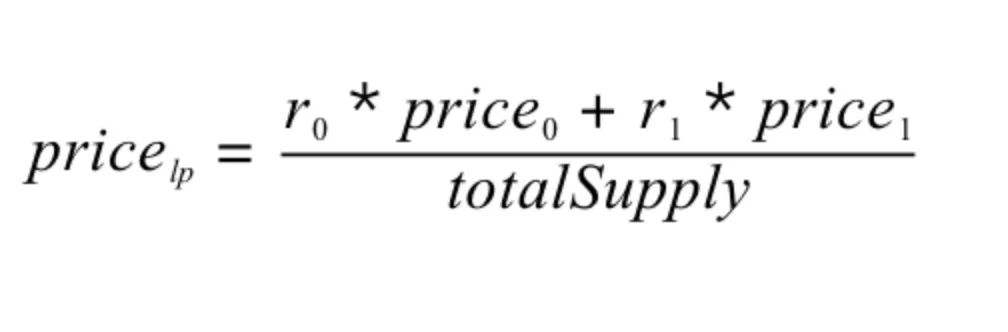
其中，r0,r1 分別代表 Uniswap 交易對中兩種代幣的存量，price0,price1 分別代表 r0 和 r1 對應代幣的價格。上面的公式簡單來說就是算出交易對中兩種代幣的總價值之和，然後除以 LP Token 的總數量，得到了單份 LP 的價值。

這個公式咋一看沒什么問題，一般來說，price0 和 price1 都會取 Uniswap 本身提供的延時價格。但是這裏存在一個被閃電貸攻擊的風險。雖然 price0 和 price1 是不能操控的，但是 r0 和 r1 卻是可以操控的。通過操控 r0 和 r1 的值，即可對整個公式進行操控。

那么有沒有辦法能獲取一種安全的 LP Token 價格，使代幣的存量無法被操控呢？Alpha Finance 團隊提供了一個思路：

根據 Alpha Finance 的分析，整個過程分為 3 步：

• 第 1 步是通過 Uniswap 的 getReserves 接口獲得交易對中對應代幣的數量，算出 K

• 第 2 步是獲取交易對中每個代幣對應的價格，然後算出代幣的價格的比例 P

• 第 3 步是通過 K 和 P 之間的關系反推真實的代幣存量。

完成以上 3 步後，最終 LP Token 的價格獲取公式會變成下面這個樣子：

這一波操作下來，好像有點整懵了，但是問題不大，我們來逐個分析。

首先，我們知道，Uniswap 採用的是恆定乘積算法。簡單來說就是 x * y = K ，也就是說，交易前後的 K 值是不會變的。在不討論手續費的情況下，K 值理論上是不會改變的。我們先記住這個前提。然後，獲取交易對中每個代幣各自的價格，比方說對 USDT 價格。這裏以 ETH-BTC 交易對為例，假設 ETH 的價格為 650 USDT，BTC 的價格為 22,000 USDT，那么 ETH/BTC 的價格比值 P 為 0.03。在得到價格的比值 P 之後，直接用第 1 步得到的 K 計算 K/P 和 K*P 就得到了對應交易對的一個正常的數量。下面要對第 3 步，即獲取正常的數量這一步進行相應的說明。

公式思路解釋

現在开始對上面的第 3 步進行說明，扶穩坐好 :D

像前面說的，恆定乘積的公式為：

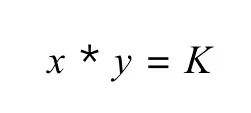
那么其實可以根據 K 來分別算出 x,y。然後根據上一節的第 2 步，我們得到了 x 和 y 的價格的比值 P。由於 Uniswap 本身是根據池中代幣的比例來確定對應的價格，所以比值 P 本身就是 x/y 的價格的比值。然後，由於 K = x * y，而 P 是由正確的價格算出的比值，那么，我們其實就可以以這個真實的 K 和 x/y 來反推真實的 x 和 y 。

推算如下：

首先，我們根據 P 和 r0,r1 的比例得出以下公式：

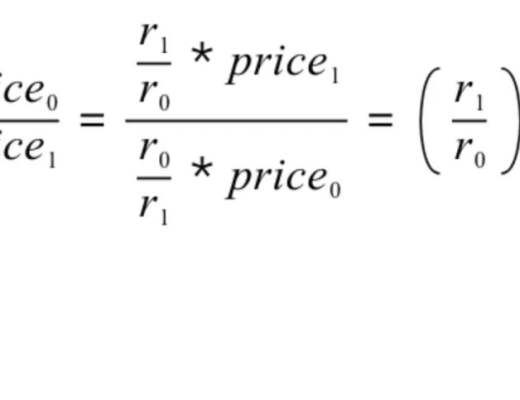
接着，根據 P 就可以倒推真實的 r0,r1，如下：

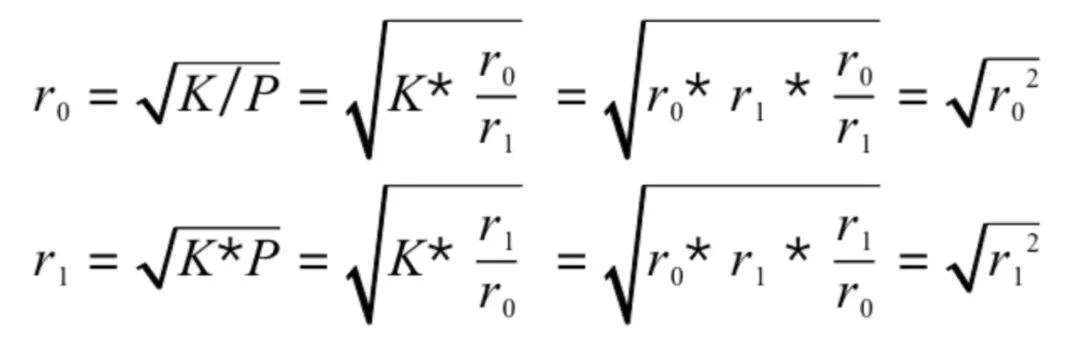
那么，拿到了正確比例的 x 和 y 之後，LP 的價格會是下面這個公式：

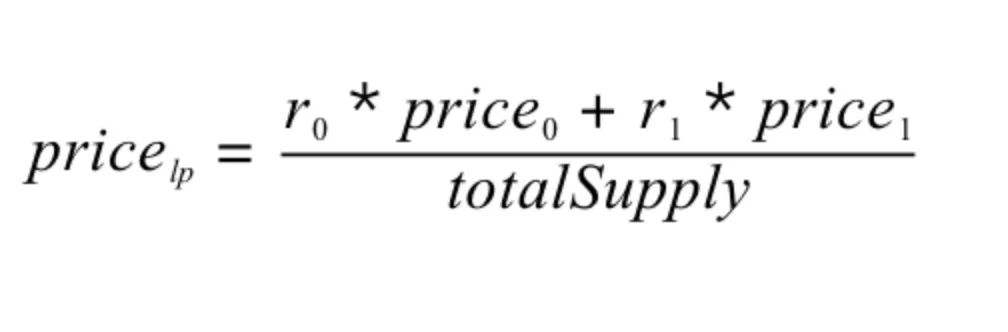
再轉換成如下：

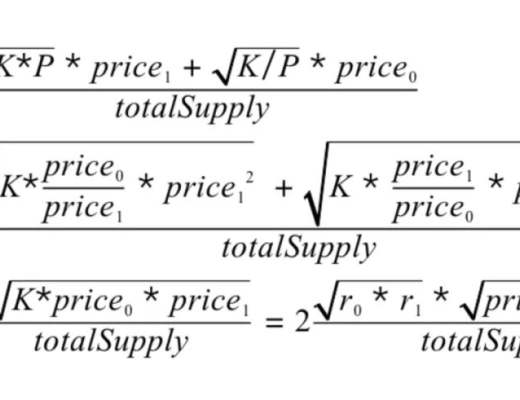
攻擊的可能性

在完成公式分析後，我們不難知道，只要有正確的價格的比例 P，就能根據這個比例倒推真實的 r0 和 r1，最後得到公式：

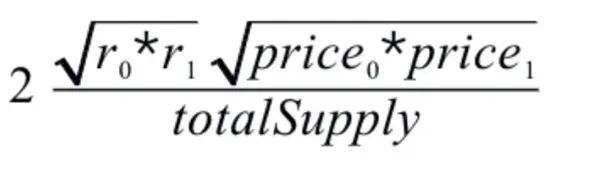
那么，這個公式能不能被攻擊呢？從公式上可以知道，公式的 price0,price1 都是可信源獲取的正確的價格，這個值是無法被操控的，然後是 totalSupply，這個值雖然可以操控，但是在控制 LP 價格進行攻擊的過程中改變 totalSupply 只能是改變你的抵押數量，這個暫時沒有用。那么剩下可以操控的只有 r0 和 r1 的值了。如何改變 r0,r1 的值呢？下面提供兩種思路進行分析：

思路一：直接進行代幣兌換

我們知道，在代幣池中，無論是採用什么算法進行計算，代幣池在進行代幣兌換的過程中，必然會發生代幣數量的改變，那么這種改變最終能不能操控公式呢？其實是不可以的。我們知道，在恆定乘積的模型中，x * y = K 總是成立的，那么也就是說無論交易過程中怎么發生代幣的兌換，K 的值總是不變的(這裏不考慮手續費的情況)，而公式中採用的是 r0 和 r1 進行相乘，所以使用代幣兌換來操控公式實際上是不可行的。

思路二：將代幣直接打入到代幣池中

這種思路比較粗暴，可以直接忽視 K 值來操控 r0 和 r1 相乘的值，但是經過我的運算，這種方法看似可行，其實是不行的。雖然達到了操控的目的，但是因為公式本身在獲取最終價格的時候採用的是根號的模式，所以最後獲得的收益是根號後的收益，比方說付出 10,000 的成本，最後只能獲得最多 100 的收益，這樣是明顯不劃算的。所以這種思路也是不可行的。

適用範圍

本算法的適用範圍僅限於適用 AMM 模型的代幣池的 LP 價格的獲取，因為整個推導過程都基於恆定乘積公式中 K 的基本特性來進行。獲取的 LP 本身所屬的交易對算法不使用 AMM 模型是不可行的，因為這種情況下，前面所有的假設都已經不成立了，那么對應的公式的推算自然也是不成立的。

總結

LP 抵押已經成為了一種迫切的需求，在目前沒有更好的方式(如 ChainLink 提供的 LP 喂價，Uniswap 提供延時 LP 接口等)，Alpha Finance 的方式可以說是一種較為安全的實現方法，使針對數量進行控制的攻擊變成不可行或成本非常高。當然，隨着越來越多場景的出現，這種算法也不一定是萬能的，項目方需要結合自身的場景，合理運用該算法，達到良好的效果。此外，特別需要注意的是，雖然公式的終極形式用的是开根號的 r0,r1 和 price0,price1 相乘，但是真正實現的時候，需要根據 K 來推導具體的 r0 和 r1 的值，不然會存在一定的誤差。

參考鏈接：

Alpha Finance 關於獲取公平  LP 價格的方法：

https://blog.alphafinance.io/fair-lp-token-pricing/

鄭重聲明：本文版權歸原作者所有，轉載文章僅為傳播信息之目的，不構成任何投資建議，如有侵權行為，請第一時間聯絡我們修改或刪除，多謝。