SignalPlus：淺談深度神經網絡

作者：Steven Wang

Deep neural networks are completely flexible by design, and there really are no fixed rules when it comes to model architecture.

-- David Foster

前言

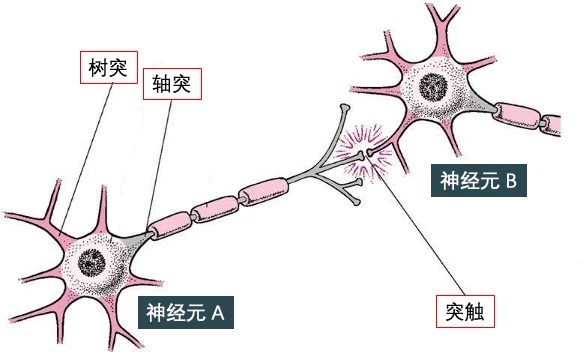
神經網絡 (neural network) 受到人腦的啓發，可模仿生物神經元相互傳遞信號。神經網絡就是由神經元組成的系統。如下圖所示，神經元有許多 樹突 (dendrite) 用來輸入，有一個 軸突 (axon) 用來輸出。它具有兩個最主要的特性：興奮性和傳導性：

• 興奮性是指當刺激強度未達到某一閾限值時，神經衝動不會發生；而當刺激強度達到該值時，神經衝動發生並能瞬時達到最大強度。

• 傳導性是指相鄰神經元靠其間一小空隙進行傳導。這一小空隙，叫做 突觸 (synapse)，其作用在於傳遞不同神經元之間的神經衝動，下圖突觸將神經元 A 和 B 連在一起。

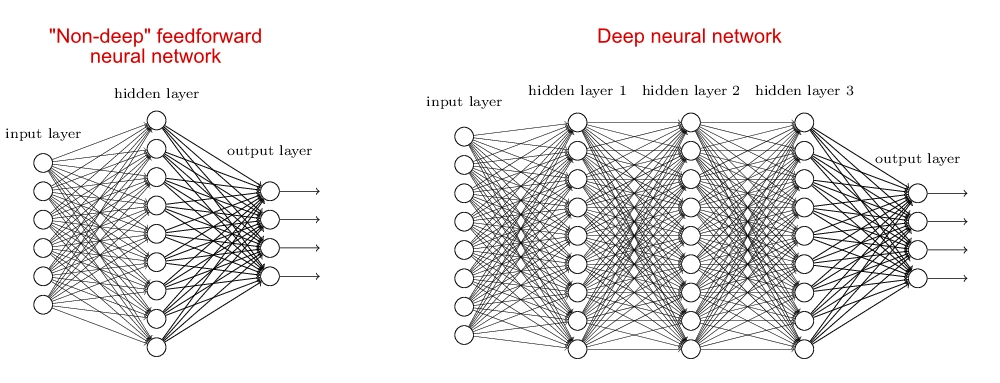
試想很多突觸連接很多神經元，不就形成了一個神經網絡了嗎？沒錯，類比到 人工神經網絡 (artificial neural network, ANN)，也是由無數的人工神經元組成一起的，比如下左圖的 淺度神經網絡 (shadow neural network) 和下右圖的深度神經網絡 (deep neural network)。

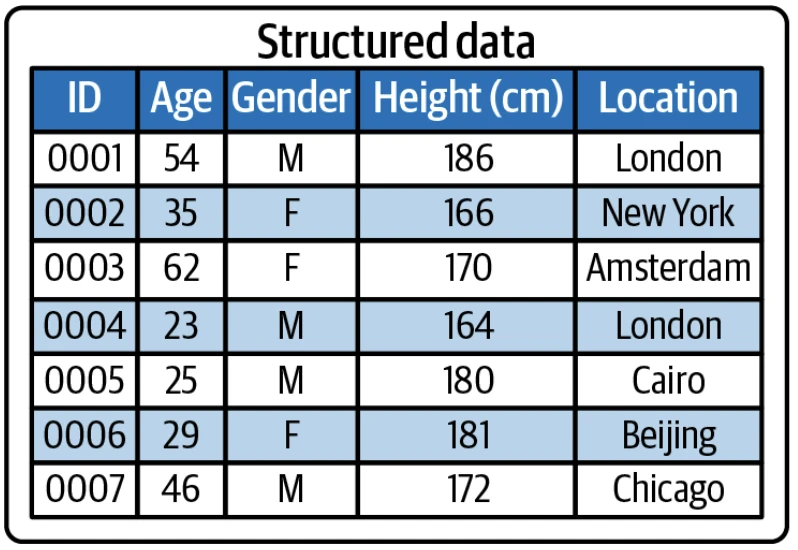
淺度神經網絡適用於 結構化數據 (structured data)，比如像下圖中 excel 裏存儲的二維數據。

深度神經網絡適用於等 非結構化數據 (unstructured data)，如下圖所示的圖像、文本、語音類數據。

生成式 AI 模型主要是生成非結構化數據，因此了解深度神經網絡是必要的。從本篇开始，我們會模型與代碼齊飛，因為

Talk is cheap. Show me the code.

-- Linus Torvalds

代碼都用 TensorFlow 和 Keras 來實現。

1.人工神經網絡

1.1 神經網絡初見

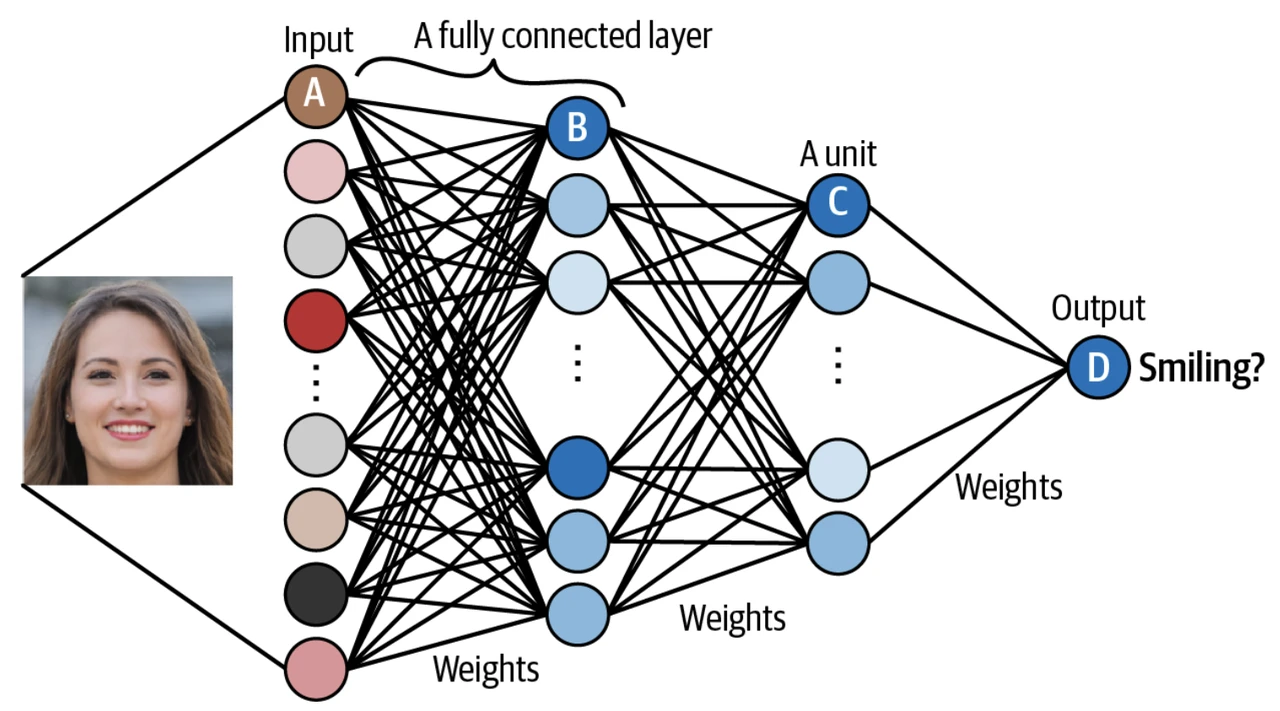
假設下面的神經網絡已經被訓練好，接着用來預測圖片中是否含有笑臉。

1. 單元 A 接收圖像裏的像素信息。

2. 單元 B 結合了輸入像素，當原始圖像中有 低級特徵 (low-level feature) 比如邊緣 (edge) 時，發出最強信號。

3. 單元 C 結合了低級特徵，當原始圖像中有 高級特徵 (high-level feature) 比如牙齒 (teech) 時，發出最強信號。

4. 單元 D 結合了高級特徵，當原始圖像中的人微笑時，發出最強信號。

當給這個神經網絡“投喂”足夠多的數據，即圖像，它會“找到”一組 權重 (weights) 使得最終預測結果盡可能准確。找權重這個過程其實就是訓練神經網絡。

對神經網絡有個初步認識之後，接下來的任務就是用 Keras 來實現它。

1.2 Keras 訓練流程

在 Keras 中實現神經網絡需要了解三大要點：

1. 模型 (models)

2. 層 (layers)， 輸入 (input) 和 輸出 (output)

3. 優化器 (optimizer) 和 損失函數 (loss)

用上面的關鍵詞來總結 Keras 訓練神經網絡的流程：將多個 層 鏈接在一起組成 模型 ，將 輸入 數據映射為預測值。然後 損失函數 將這些預測值 輸出 ，並與目標進行比較，得到損失值 (用於衡量網絡預測值與預期結果的匹配程度)， 優化器 利用這個損失值來更新網絡的權重。

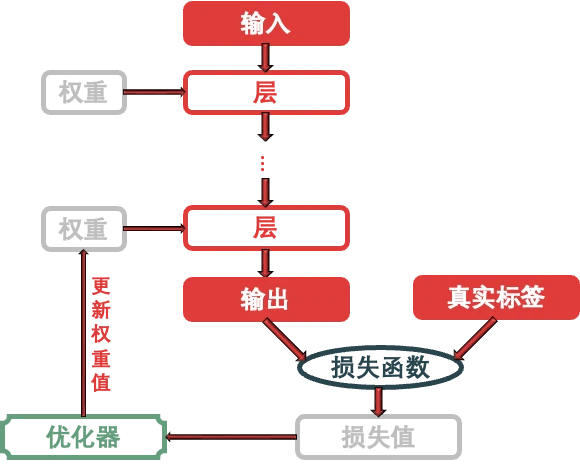
到此終於可以展示點代碼了，即便是引入工具庫。首先從 tensorflow.keras 庫中用於搭建神經網絡的模塊。

整個神經網絡就是一個模型，大框架的代碼都來自 models 模塊；模型是由多個層組成，而不同的層的代碼都來自 layers 模塊；模型的第一層是輸入層，負責接入輸入，模型的最後一層是輸出層，負責提供輸出，一頭一尾都在 models 模塊；模型骨架好了，要使它中看又中用就需要 optimizers 模塊來訓練它了。

1.3 極 簡神經網絡

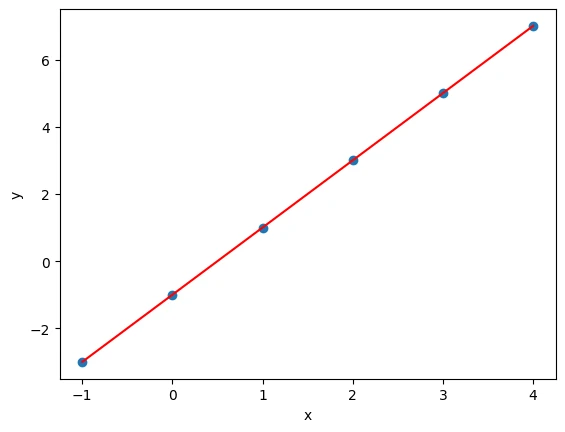
學過機器學習的同學遇到的第一個模型一定是线性回歸，還是單變量的线性回歸。給定一組 x 和 y 的數據：

x = [-1,  0, 1, 2, 3, 4 ]

y = [-3, -1, 1, 3, 5, 7 ]

找出 x 和 y 之間的關系，當 x new = 10 時，問 y new 是多少？

如下圖所示，將 x 和 y 以散點的形式畫出來，不難發現下圖的紅线就是 x 和 y 之間的關系。現在想用 Keras 殺雞用牛刀的構建一個神經網絡來求出這條紅线。

1.3.1 創建模型

用一層含一個神經元的神經網絡即可，代碼如下：

首先用 models. Sequential() 創建一個空神經網絡，然後不斷添加層，這裏我們添加了 layers. Dense() ，叫做稠密層。函數裏面的參數 input_shape=[ 1 ] 表示輸入數據的維度為 1 ，units= 1 表示輸出只有 1 個神經元。可視化如下：

1.3.2 檢查模型

檢查一下模型信息，奇怪的是參數個數 (下圖 Param #) 居然是 2 個而不是 1 個。因為從上圖來看 y = wx ，只應該有 w 一個參數啊。

原因是在計算每層參數個數時，每個神經元默認會連接到一個值為 1 的 偏置單元 (bias unit)，因此其實上圖更准確的樣子如下：

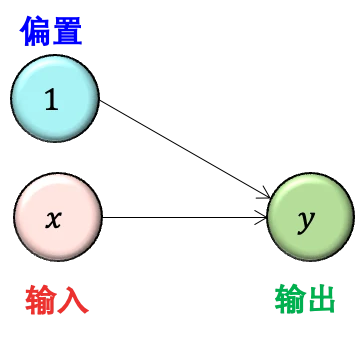
這樣就對了，此時 y = wx +b，有 w 和 b 兩個參數了。

嚴格來說，其實 Dense() 函數裏還是一個參數叫 activation，它字面意思是激活函數，本質上做的事情是將 wx +b 以非线性的模式轉換再賦予給 y 。如果定義激活函數為 g ，那么 y = g(wx +b)。在 Keras 如果不給 activation 指定值，那么就不需要做任何非线性轉換。加上激活函數這個概念，我們給出一個完整的圖：

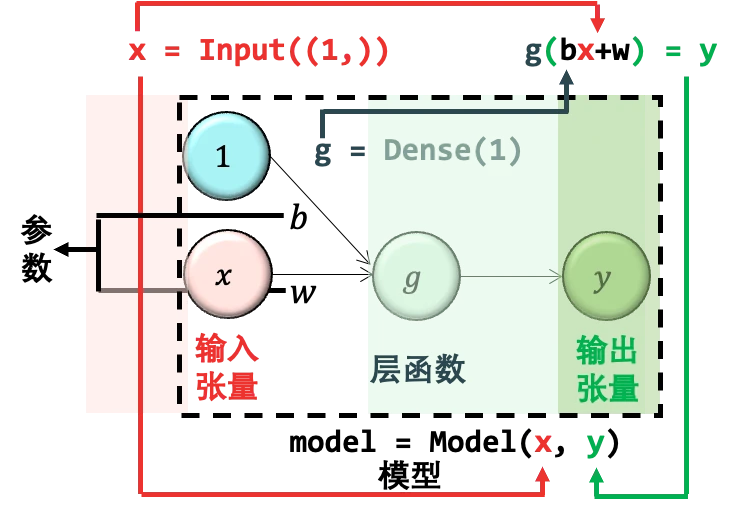
我們的目標就是求出上圖中的參數，權重 w 和偏置 b。

1.3.3 編譯模型

模型框架搭好後，接着就是優化問題了，在下面 complie() 函數設定參數 ，即指定優化方法為隨機梯度下降 ，設定參數 ，即制定損失函數用均方誤差函數。

1.3.4 訓練模型

訓練模型用 fit() 函數，把數據 x 和 y 傳進去。值得注意的是參數 epochs= 500 ，epoch 中文是期，即整個訓練集被算法遍歷的次數，這裏就是遍歷 500 次模型訓練結束。

打印出首尾 5 期的信息，不難發現一开始 loss 很大 13.4237 ，到最後 loss 非常小只有 3.8166 e-05 ，說明在訓練集裏的預測值和真實值幾乎一致。

模型訓練之後可以用 get_weights() 函數來檢查參數。

返回結果第一個是權重 w ，第二個偏置 b ，因此該神經網絡模型就是 y = 1.9973876 x - 0.99190086 ≈ 2 x - 1 。

1.3.5 評估模型

評估模型用 predict() 函數，將新數據 x_new 傳進去，得到結果 8.995028 ，非常接近 2*x_new - 1 = 9 。

從下圖可看出，神經網絡從 6 個數據 (深青點) 中“學到”了模型 (紅线)，而該模型可用在新數據 (藍點) 上。

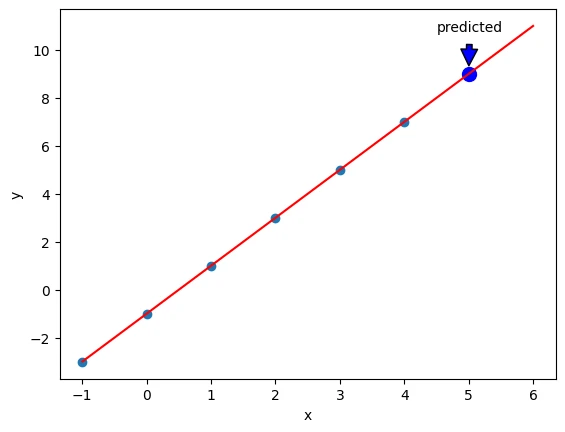
總結一下神經網絡全流程：

1. 創建模型 ：用 Sequential() ，當然還有其他更好的方法，下節講。

2. 檢查模型 ：用 summary()

3. 編譯模型 ：用 compile()

4. 訓練模型 ：用 fit()

5. 評估模型 ：用 predict()

雖然本例構建了一個極簡神經網絡，但是五大步驟一個不少，構建復雜的神經網絡也需要這五步，區別在於第 1 步創建模型時要拼接很多層，第 5 步要選擇更先進的優化器，但萬變不離其宗。下兩節就來看看兩個稍微復雜的神經網絡，分別是 前 反饋神經網絡 (feedforward neural network, FNN) 和 卷積神經網絡 (convoluational neural network, CNN)。

2. 前饋神經網絡(FNN)

上節的極簡神經網絡太無聊了，但是主要是用來明晰 Keras 裏神經網絡的概念而步驟，下面來看看神經網絡做一些有趣的事情，預測圖像類別。首先看看使用的數據集 CIFAR-10 (https://www.cs.toronto.edu/~kriz/cifar.html)。

該數據集共有 60, 000 張彩色圖像，這些圖像是 32* 32 ，分為 10 個類，每類 6000 張圖。其中 50, 000 張圖像用於訓練，另外 10, 000 用於測試。下圖就是列舉了 10 個類，每一類隨機展示的 10 張圖片：

用模塊 datasets 裏的 load_data() 函數來下載數據並對圖像的像素做歸一化，原來像素在 0 到 255 之間，現在歸一到 0 到 1 之間。

對於類別，用模塊 utils 裏的函數 to_categorical() 函數對類別進行獨熱編碼 (one-hot encoding)。思路就是把整數用只含一個 1 的向量表示，比如類別 5 經過獨熱編碼後變成 [ 0, 0, 0, 0, 1, 0, 0, 0, 0, 0 ]，該向量有 10 個元素，和類別個數一致，向量只有第 5 個元素是 1 (獨熱?)，其他都是 0 (好冷?)。

訓練集的前十張圖片展示如下：

2.1 創建模型

2.1.1 序列式

上節已經見識過序列式 (sequential) 建模了，首先用 models. Sequential() 創建一個空神經網絡，然後不斷添加層。本例中有一個打平層 layers. Flatten() 和三個稠密層 layers. Dense()。

上面代碼給出下圖所示的模型：

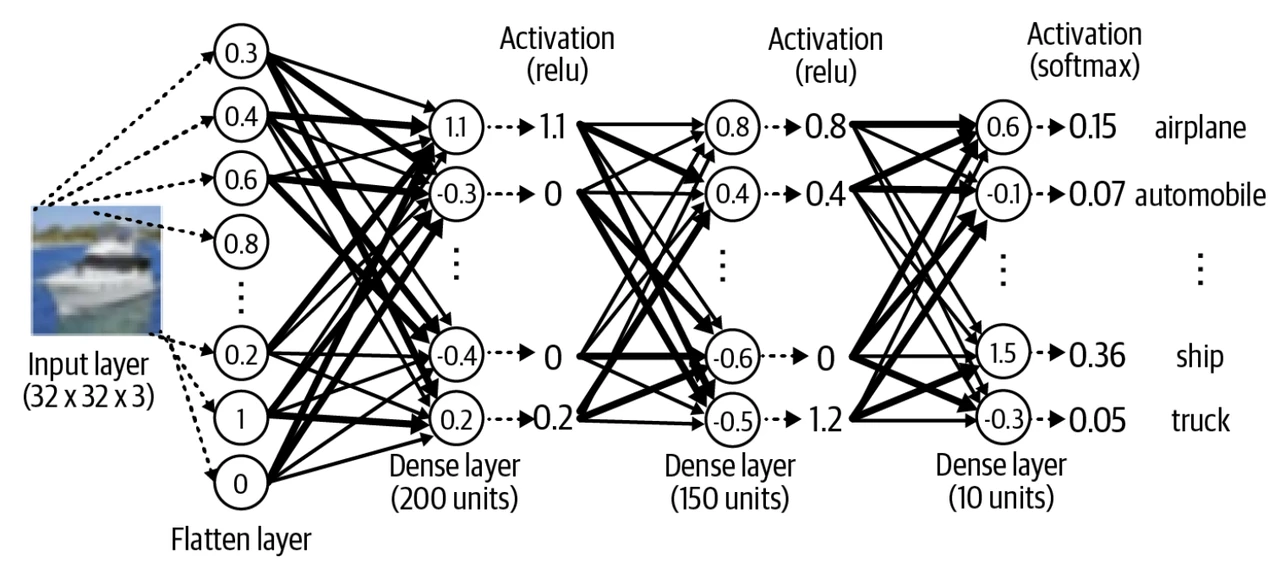
有了感官認識，再來研究代碼。為什么需要打平層？因為圖像有寬，高，色道三個維度，而打平到一維的過程如下圖所示。

原始圖像 ( 32, 32, 3) 輸入打平層 (在參數 input_shape 指定圖像維度大小)，打平之後變成了一個 32* 32* 3 = 3072 的向量，可以想成現在輸入有 3072 個神經元。之後三個稠密層的

• 神經元個數 (參數 units) 分別為 200, 150 和 10 ，前兩個 200 和 150 是隨便給的或者當成超參數調試出來，但最後一個 10 是和類別的個數一致。

• 用到的激活函數 (參數 activation) 分別是 relu, relu 和 softmax，前兩個 relu 幾乎是標配，但最後一個 softmax 和任務相關，如果是多分類問題就用 softmax。

常用的 激活函數 (activation function) 如下圖所示：

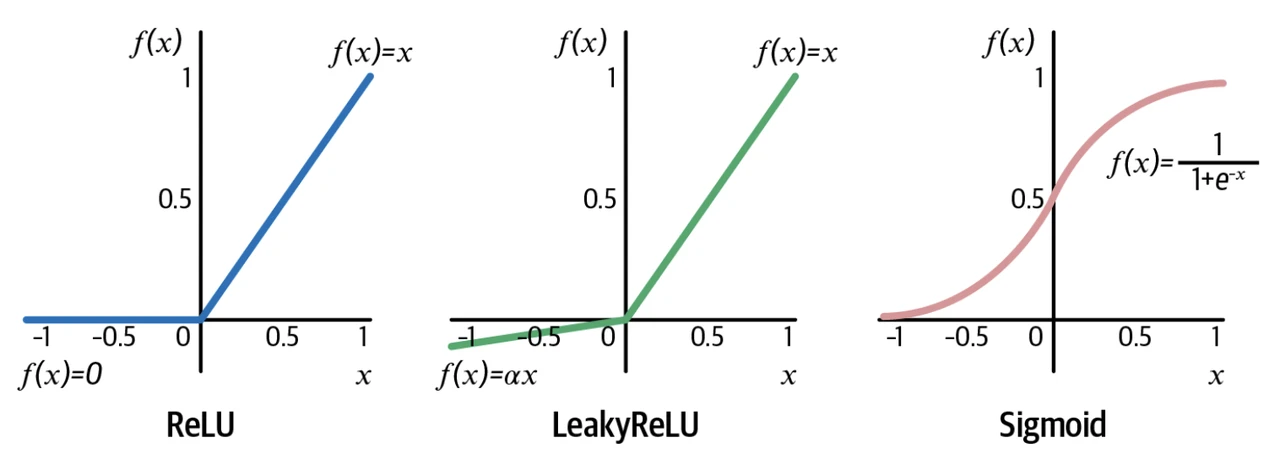
ReLU 將負輸入 (x < 0) 轉換成 0 ， 正輸入 (x > 0) 保持不變。LeakyReLU 和 ReLU 非常相似，唯一區別就是對於負輸入 (x < 0)，轉換的結果也是一個和輸入相關的負數 (ax)。

Sigmoid 將實數轉換成 0-1 之間的數，而這個數可當成概率，因此 Sigmoid 函數用於二分類問題，它的延伸版 Softmax 函數用於多分類問題。

2.1.2 函數式

在實操中，我們更習慣用 函數式 (functional) 建模。序列式構建的模型都可以用函數式來完成，反之不行，如果在兩者選一，建議只用函數式來構建模型。代碼如下：

函數式建模只用記住一句話： 把層當做函數用 。有了這句在心，代碼秒看懂。

• 第 1 行，用 Input() 接收圖像數據。

• 第 2 行，把 Flatten() 當成函數 f ，化簡不就是 x = f(input)

• 第 3 行，把 Dense (units= 200, activation='relu') 當成函數 g ，化簡不就是 x = g(x)

• 第 4 行，把 Dense (units= 150, activation='relu') 當成函數 h ，化簡不就是 x = h(x)

• 第 5 行，把 Dense (units= 10, activation='softmax') 當成函數 q ，化簡不就是 output = q(x)

這樣一層層函數接着函數把 input 傳遞到 output，output = q(h(g(f(input))))，最後再用 models. Model 將它倆建立關系。

2.2 檢查模型

當模型創建之後和使用之前，最好是檢查一下神經網絡每層的數據形狀是否正確，用 summary() 函數就能幫你打印出此類信息。

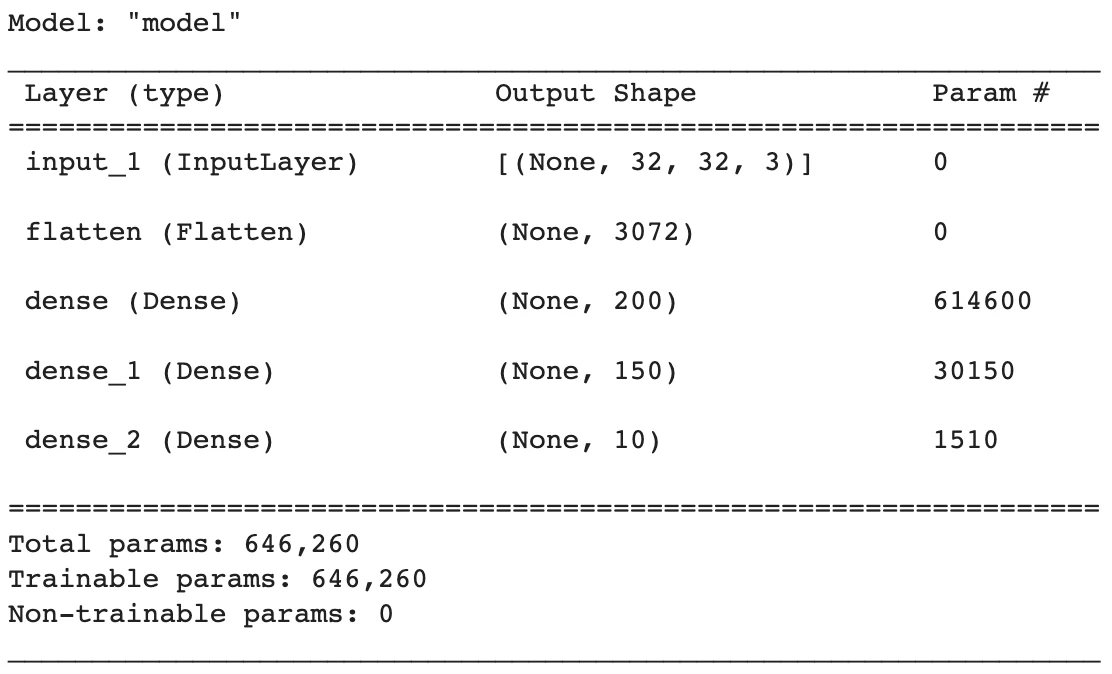
該模型自動被命名 “model”，接着一張表分別描述每層的名稱類型 (layer (type))、輸出形狀 (Output Shape) 和參數個數 (Param #)。我們一層層來看

• InputLayer 層被命名成 input_ 1 ，輸出形狀為 [None, 32, 32, 3 ]，後面三個元素對應着圖像寬、高和色道，第一個 None 其實代表的樣本數，更嚴謹的講是一批 (batch) 裏面的樣本數。為了代碼簡潔，這個樣本數在建模時通常不需要顯性寫出來。

• Flatten 層被命名成 flatten， 3072 就是 32* 32* 3 打平之後的個數，參數個數為 0 ，因為打平只是重塑數組，不需要任何參數來完成重塑動作。

• 第一個 Dense 層被命名為 dense，輸出形狀是 200 ，參數 614, 600 = ( 3072 + 1) * 200 ，不要忘了有偏置單元。

• 第二個 Dense 層被命名為 dense_ 1 ，輸出形狀是 150 ，參數 30, 150 = ( 200 + 1) * 150 ，同樣考慮偏置單元。

• 第三個 Dense 層被命名為 dense_ 2 ，輸出形狀是 10 ，參數 1, 510 = ( 150 + 1) * 10 ，同樣考慮偏置單元。

最下面還列出總參數量 (Total params) 646, 260 ，可訓練參數量 (Trainable params) 646, 260 ，不可訓練參數量 (Non-trainable params) 0 。為什么還有參數不需要訓練呢？你想想遷移學習，把借過來的網絡鎖住开始的 n 層，只訓練最後 1- 2 層，那前面 n 層的參數可不就不參與訓練嗎？

2.3 編譯模型

當構建模型完畢，接着需要編譯模型，需要設定三點：

1. 根據要解決的任務來選擇損失函數

2. 選取理想的優化器

3. 選取想監控的指標

編譯模型用 complie() 函數，代碼如下：

在 complie() 函數中：

• 對於參數 loss，本例是十分類問題，因此用的損失函數是 categorical_crossentropy，此外：

• 二分類問題：損失函數是 binary_crossentropy

• 回歸問題：損失函數是 mean_squared_error

• 對於參數 optimizer，大多數情況下，使用 adam 和 rmsprop 優化器及其默認的學習率是穩妥的。在設定該參數時，也可以通過用名稱和實例化對象來調用。

• 名稱：'sgd'

• 對象：optimizers.Adam(learning_rate= 0.0005)

• 對於參數 metrics，也可以通過用名稱和實例化對象來調用，在本例中的指標是精度，那么可寫成

• 名稱：['accuracy']

• 對象：[metrics.categorical_accuracy]

注意，指標不會影響模型的訓練過程，只是讓我們監控模型訓練時的表現，損失函數才會影響模型的訓練過程。

2.4 訓練模型

訓練模型不是把所有數據一起丟進去，而是按批量丟進去。在介紹訓練模型前，需要明晰幾個概念：

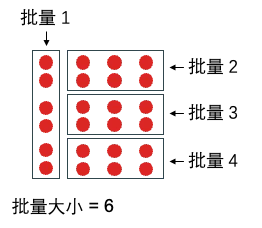
• 批量大小 (batch size) 指一個批量裏的樣本個數。下例中總共有 24 個數據，如果每個批裏有 6 個數據，那么總局可分成 4 批。

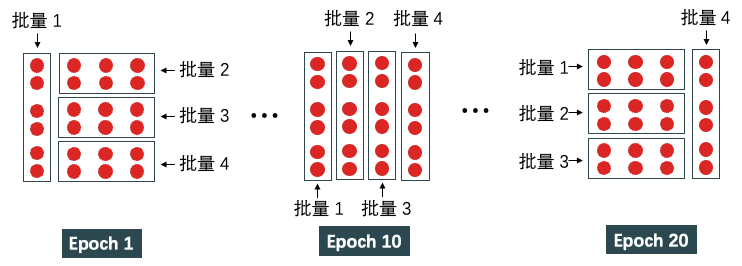
• 期 （epoch）指整個訓練集被算法遍歷一次。當設 epoch 為 20 時，那么要以不同的方式遍歷整個訓練集 20 次。一次 epoch 要經歷 4 次迭代才能遍歷整個數據集，即樣本總數 / 批量大小 = 24 / 6 次迭代。20 次 epoch 運行過程如下圖所示。

訓練模型用 fit() 函數，代碼如下：

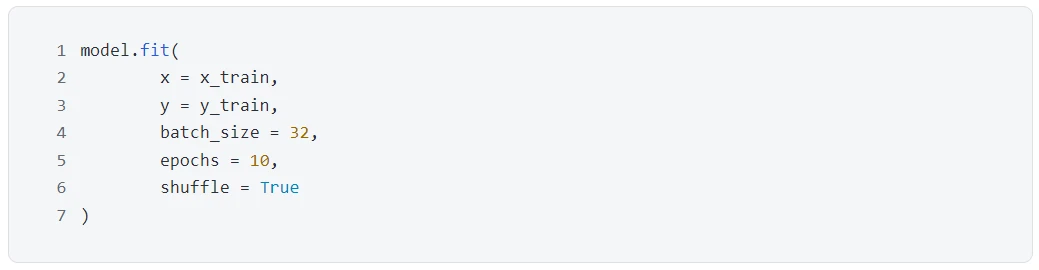
上圖給出訓練步驟，不難看出訓練集被分成 1563 個堆，每堆含 32 張圖 (batch size)。10 個 epoch 之後， 損失函數 (categorical cross-entropy) 從 1.8472 降到 1.3696 ，同時 准確率 (accuracy) 從 33.41% 提升到 51.39% 。模型在訓練集上可以到達 51.39% 的准確率，那么它在沒見過的數據集上的表現會如何呢？

2.5 評估模型

用 evaluate() 函數直接看准確率。

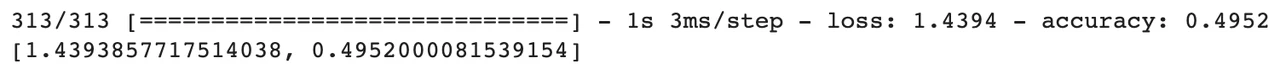
模型在測試集上的准確率為 49.52% ，比隨機預測一個類別的准確率 10% 高多了 (因為有十類)。由於我們用這樣一個非常簡單的前饋神經網絡來預測圖片類別， 49.52% 的准確率已經算是不錯的結果了。

用 predict() 函數比對預測和真實類別。

測試集裏用 10, 000 張圖，類別是 10 個，因此 preds 是一個 [ 10000, 10 ] 的數組，每一行都是模型對相應圖片預測的 10 個類別的概率，當然所有概率加起來等於 1 。看看測試集裏第一張圖片的預測結果：

y_test 也是一個 [ 10000, 10 ] 的數組，每一行都是相應圖片真實的類別，因此 10 個元素有 9 個零和 1 個一。看看測試集裏第一張圖片的真實類別：

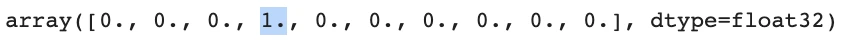
不難看出，預測結果 preds[ 0,:] 中類別四的概率最高 0.38579068 ，而真實類別 test[ 0.:] 就是類別四 (第 4 個元素是一)。用 np.argmax 分別從預測結果 preds[ 0,:] 和真實類別 test[ 0.:] 中找到最大值對應的索引，並從 CLASSES 中映射出類別描述。

測試集第一張是貓，而模型預測的也是貓，做對了！

再試試第四張。

測試集第四張是船，但模型預測的是飛機，做錯了！

可視化：上面的對比方法太麻煩，我們可以隨機抽取測試集裏的 10 張，打印出每張圖片，在圖片下還貼上模型預測類別和其真實類別。

從上面 10 張小圖可看出，模型預測正確了 5 張，正確率 50% ，和之前統計出來的 49.52% 吻合。雖然這只是一個用於預測的判別模型，但當我們創建生成模型時，本節介紹的內容 (比如層、激活函數和優化器等) 仍然適用。

下一步來看看如何用卷積神經網絡來改進模型。

3. 卷積神經網絡（CNN）

前饋神經網絡 (FNN) 在圖像分類問題上表現差的根本原因是它沒有考慮到圖像的空間結構，比如圖像中的相鄰像素都很接近，而 FNN 一开始直接將像素打平，破壞圖像特有的空間結構。我們需要更適合圖像的神經網絡，比如卷積神經網絡 (CNN)。

3.1 基本概念

假設在黑夜你面前出現一張巨幅圖片，黑暗中你看不出來是輛車，你只能用手電筒一點一點掃過，把每次掃過看到的東西投影到下一層，以此類推。比如第一層你看到一些橫线豎线斜线，第二層組合成一些圓形方形，第三層組合成輪子車門車身，第四層組合成一輛車。這樣就能用個手電筒在黑夜裏辨別出照片裏有輛車了。

上例其實就是一個卷積神經網絡識別圖像的過程了，首先明晰幾個定義：

• 濾波器 (filter)：在輸入數據的寬度和高度上滑動，與輸入數據進行卷積，就像上例中的手電筒。

• 卷積 (convolution)：在這裏的定義就是把所有“濾波器的像素”乘以“濾波器掃過圖片的像素”再加總。

• 步長 (stride)：遍歷圖像時濾波器的步長，默認值為 1 ，既濾波器每次移動一個像素。

• 填充 (padding)：有時候會將輸入數據用 0 在邊緣進行填充，可以控制輸出數據的尺寸 (最常用的是保持輸出數據的尺寸與輸入數據一致)。

卷積 (Convolution)

卷積神經網絡的最大特點當然是卷積操作了。回顧上面的定義，將“濾波器的像素”乘以“濾波器掃過圖片的像素”再加總，看下面兩個例子，假設濾波器的大小是 3* 3 。

第一張圖片和濾波器的卷積為 0.6* 1 + 0.4* 1 + 0.6* 1 + 0.1* 0 + (-0.2)* 0 + (-0.3)* 0 + (-0.5)*(-1) + (-0.4)*(-1) + (-0.3)*(-1) = 2.8 。

第二張圖片和濾波器的卷積為 (-0.7)* 1 + 0.6* 1 + 0.2* 1 + 0.1* 0 + 0.5* 0 + (-0.3)* 0 + (-0.3)*(-1) + (-0.4)*(-1) + 0.5*(-1) = -0.1 。

當卷積值越 正 ，說明濾波器和圖片越 相符 ；當卷積值越 負 ，說明濾波器和圖片越 不符 。上例中第一張圖片和濾波器的卷積值為 2.8 ，兩者 相符 ；第二張圖片和濾波器的卷積值為 -0.1 ，兩者 不符 。

濾波器 (Filter)

濾波器的作用就是濾波，即過濾掉一些信息，等價於提取保留下的信息。下面代碼創建兩個 3* 3 大小的濾波器，filter 1 能提取圖像中的水平线，filter 2 能提取圖像中的豎直线。注意這裏 1 代表黑， 0 代表灰，-1 代表白色。

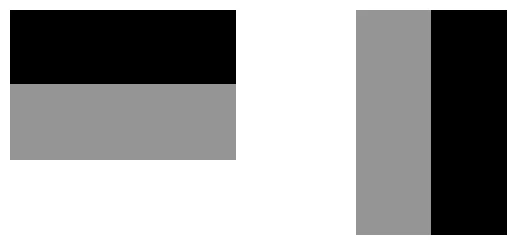
下面看一個如何用這兩個濾波器來提取信息的，原始圖片如下：

不難發現，filter 1 的確從圖像中提取到水平的邊緣信息，比如杯子口的上下沿。

不難發現，filter 2 的確從圖像中提取到豎直邊緣的信息，比如杯子口的左右沿。

有了濾波器的加入，我們可以創建 卷積層 (convoluational layer) 了。卷積層本質上就是一組濾波器，下例中個數是 2 個，而濾波器中的元素值稱為權重 (weights)，是通過訓練 CNN 學到的。

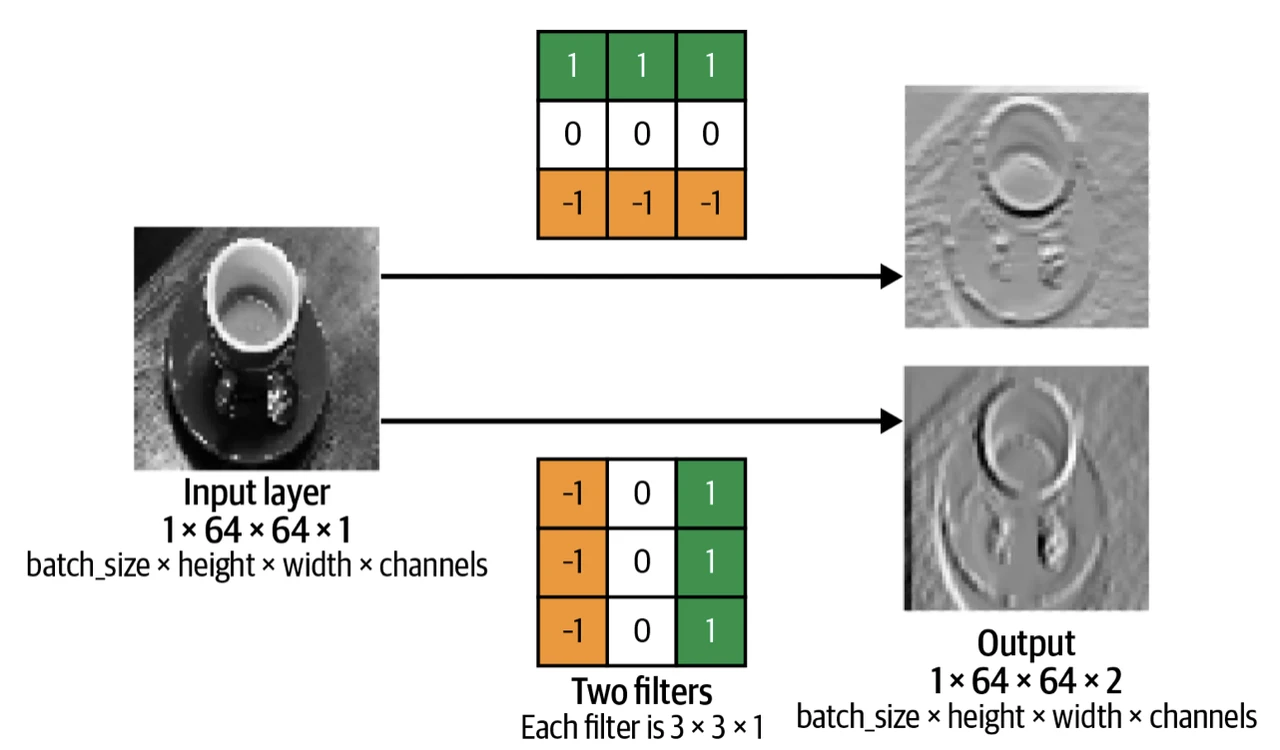
在 Keras 中用 layers .Con v 2 D() 來創建卷積層。這裏黑白相片是 64* 64* 1 (色道只有 1 個)，而濾波器有兩個 (參數 filters 設置為 2)，濾波器大小是 3* 3 (參數 kernel_size 設置為 ( 3, 3))。

還有兩個參數 strides 和 padding 是什么東西？

步長 ( Stride )

步長是濾波器遍歷圖像時移動的像素個數，默認值為 1 ，既濾波器每次移動一個像素。當步長為 2 時，不難想象輸出圖像大小只有輸入圖像大小的一半。

填充 (Padding)

顧名思義，填充就是在圖像四周添加元素。當 padding = "same" 時，配着 strides = 1 ，可以保證輸出圖像和輸入圖像的大小一樣。下圖輸入圖像大小是 5* 5 (藍色圖片)，填充之後圖像大小變成 7* 7 (帶白色的圖片)，濾波器大小是 3* 3 (灰色)，輸出圖像大小還保持 5* 5 (綠色圖片)。

弄清楚組成卷積層的元素之後，我們可以像上節拼接稠密層一樣來拼接卷積層。

3.2 拼接卷積層

先看一段代碼：

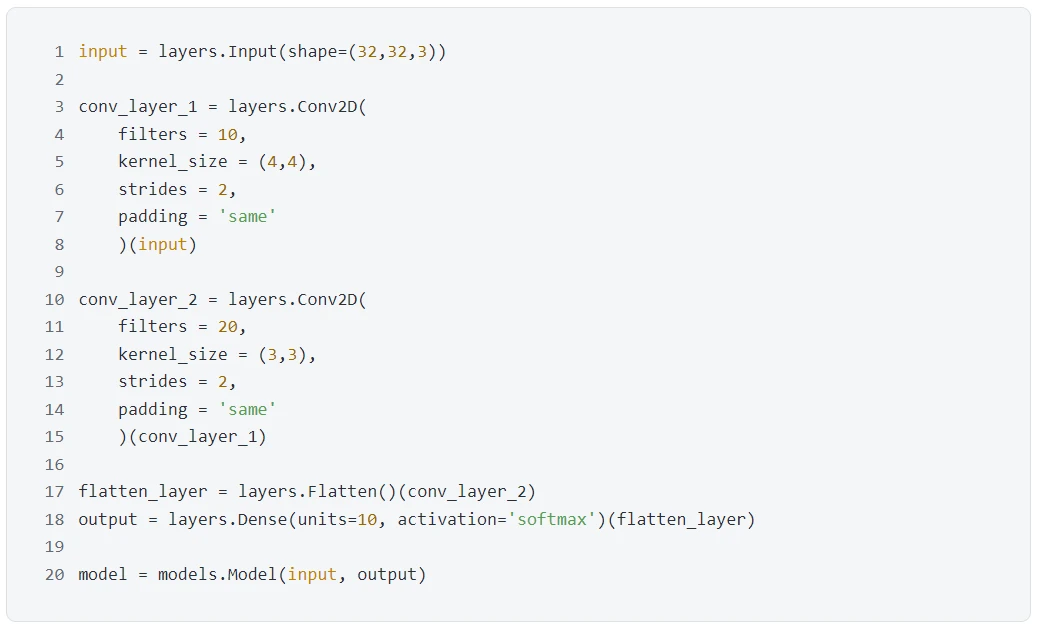
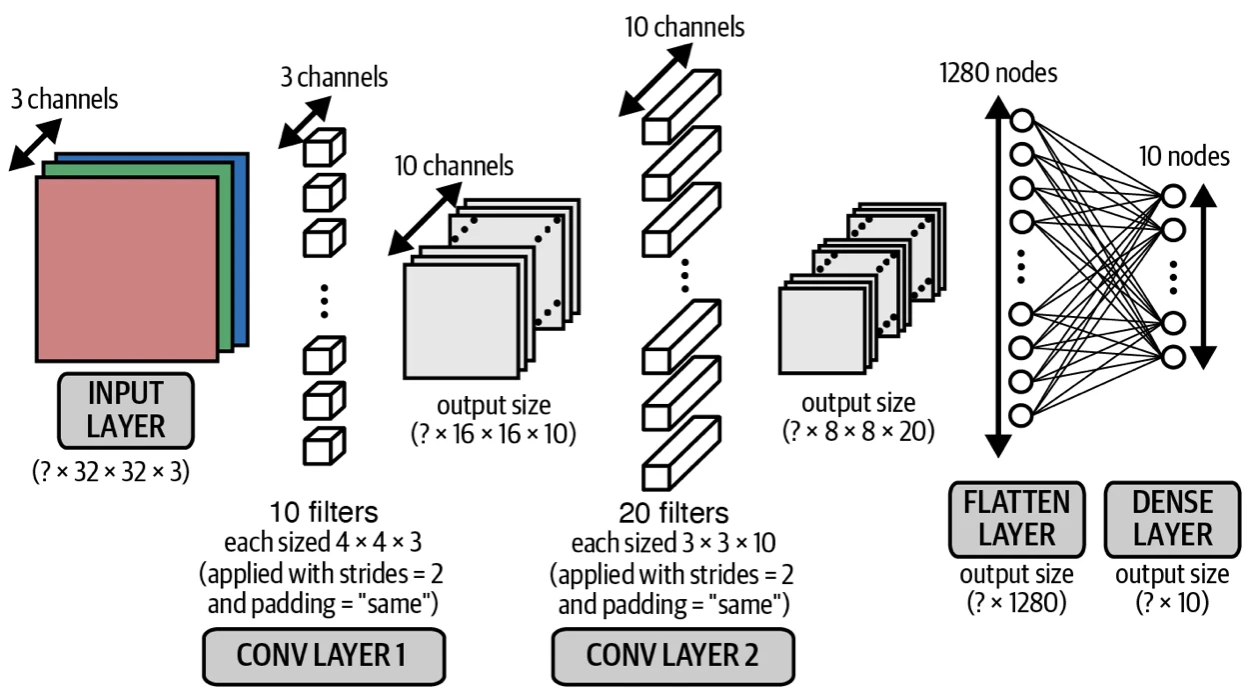
上段代碼對應着下圖的樣子。

上面每個卷積層輸出的大小讓人眼花繚亂，如果用 n I 代表輸入圖像的大小， f 代表濾波器的大小， s 代表步長， p 代表填充層數， n O 代表輸入圖像的大小，那么有以下關系：

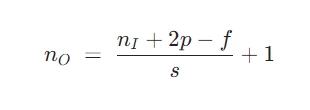
用這個公式來驗證第一個和第二個卷積層的輸出的寬度和高度：

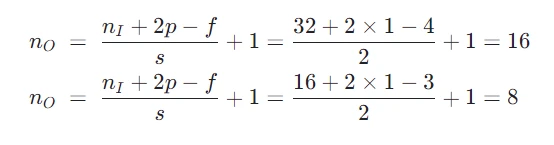
最重要的東西來了， 卷積層的輸出色道等於濾波器個數 (即代碼裏面的參數 filters) 。一個直觀理解是每個濾波器並行在“掃描”圖片做卷積，那么最終產出一定有一個維度大小是濾波器的個數。

檢查一下模型。

該模型自動被命名 “model”，接着一張表分別描述每層的名稱類型 (layer (type))、輸出形狀 (Output Shape) 和參數個數 (Param #)。我們一層層來看

• InputLayer 層被命名成 input_ 1 ，輸出形狀為 [None, 32, 32, 3 ]，後面三個元素對應着圖像寬、高和色道，第一個 None 其實代表的樣本數，更嚴謹的講是一批 (batch) 裏面的樣本數。為了代碼簡潔，這個樣本數在建模時通常不需要顯性寫出來。

• 第一個 Con v 2 D 層被命名為 con v 2 d，輸出形狀是 [None, 16, 16, 10 ]，參數 490 = ( 4* 4* 3 + 1) * 10 ，首先不要忘了有偏置單元，其次 4* 4 是濾波器的大小， 3 是輸入的色道個數，因此我們需要 4* 4* 3 個權重來描述每個濾波器，一共有 10 個。

• 第二個 Con v 2 D 層被命名為 con v 2 d_ 1 ，輸出形狀是 [None, 8, 8, 20 ]，參數 1, 820 = ( 3* 3* 10 + 1) * 20 ，首先同樣考慮偏置單元，其次 3* 3 是濾波器的大小， 10 是輸入的色道個數，因此我們需要 3* 3* 10 個權重來描述這個濾波器，一共有 20 個。

• Flatten 層被命名成 flatten， 1, 280 就是 8* 8* 20 打平之後的個數，參數個數為 0 ，因為打平只是重塑數組，不需要任何參數來完成重塑動作。

• 最後一個 Dense 層被命名為 dense，輸出形狀是 10 ，參數 12, 810 = ( 1280 + 1) * 10 ，同樣考慮偏置單元。

最下面還列出總參數量 (Total params) 15, 120 ，可訓練參數量 (Trainable params) 15, 120 ，不可訓練參數量 (Non-trainable params) 0 。

到此一個 CNN 已經基本建成，我們再添加兩個技巧使得 CNN 效果更好： 批量歸一 (batch normalization) 和 隨機失活 (dropout)。

3.3 批量歸一

在訓練 CNN 時，模型成功關鍵時要確保權重保持在一定的範圍內，要不然會出現梯度爆炸 (exploding gradient) 的情況。批量歸一可以解決此問題，它在每層都會按批 (mini-batch) 計算數據的 均值 (mean) 和 標准差 (standard deviation)，然後在每個數據上減去均值除以標准差。為了“還原”數據，我們需要“學習”兩個參數，放縮參數 γ 和平移參數 β 。

批量歸一的算法如下：

Keras 中用 BatchNormalization() 來實現批量歸一層。批量歸一層一般放在稠密層或卷積層之後。

函數中參數 momentum 用於計算移動均值和移動標准差，這個是為了在預測的時候使用。因為預測通常在一個數據上，這時無法計算均值和標准差，那么只能利用在訓練時計算的移動均值和移動標准差。

3.4 隨機失活

隨機失活的靈感來自考試。通常考試前，學生會做往年的卷子來學習知識點。有的學生死記硬背來解題，這樣到了實際考試中就會表現不好，因為他們沒有真正理解知識點。好的學生會通過卷子來理解通用的知識點，這樣出現新題也能正確解答。

同理，為了讓神經網絡不要“死記硬背”，我們可以隨機讓某些神經元失活，即使得它們的輸出為 0 ，如下圖所示。

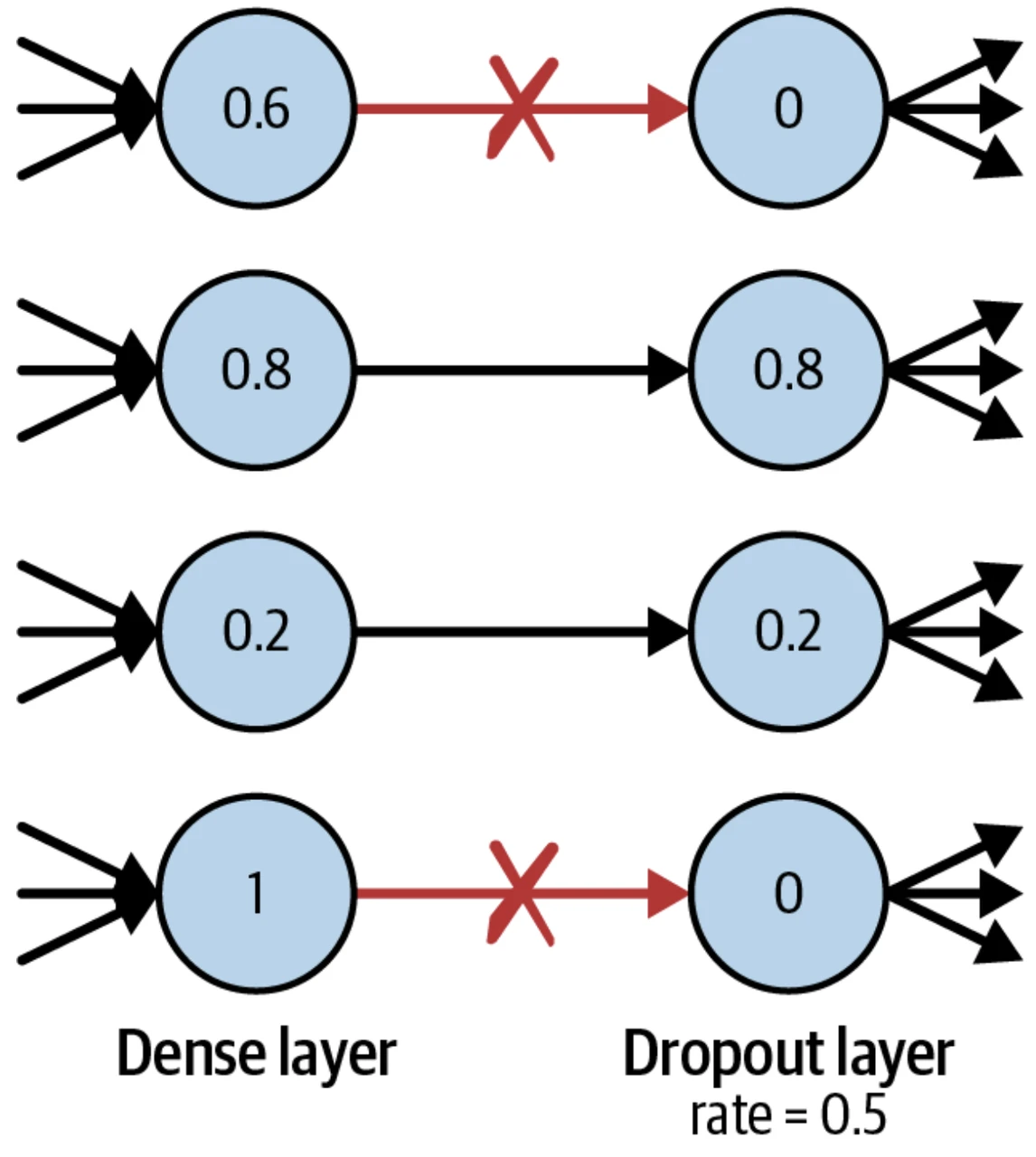
在預測過程中，神經元不失活，因此用完整的神經網絡做預測。

Keras 中用 Dropout() 來實現失活層。失活層一般放在稠密層之後。

函數中參數 rate 用於設定失活神經元的比率，比如本例中 25% 的神經元失活了。

3.5 完整模型

現在我們可以在之前的 CNN 加上批量歸一層和失活層來完善模型了。

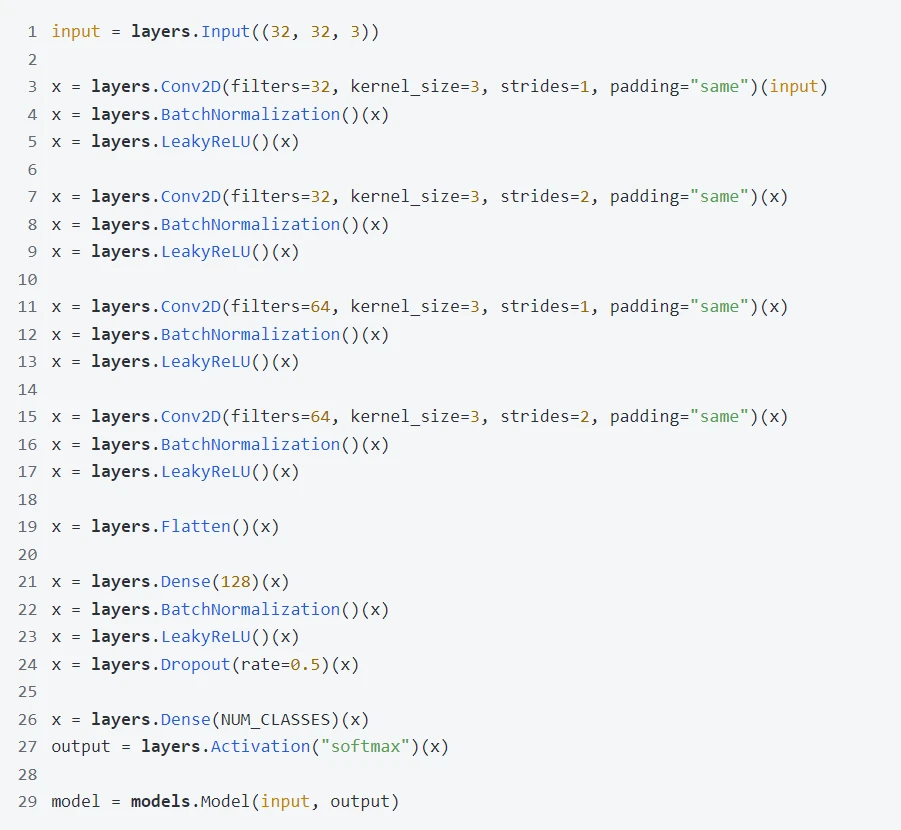
再看上面的代碼是不是很好理解了，該 CNN 中有四個卷積層，每個後面接一個批量歸一層和一個 LeakyReLu 層。注意 Keras 裏時萬物皆可作為層，甚至像激活函數也可以用層的形式實現。接着用一個打平層將數據打平，接一個稠密層，個批量歸一層，一個 LeakyReLu 層，一個失活層和一個稠密層，最後用 softmax 以概率的形式輸出。

檢查一下這個完善後的 CNN 模型。

我們發現激活層都不包含參數，因為就是一個轉換；打平層和失活層也不包含參數，這個也很好理解；對於卷積層和稠密層的參數量，之前已經解釋過算法；對於批量歸一層，對於每個 channel 需要學習放縮參數 γ 和平移參數 β ，以及移動均值和移動標准差，這樣包含參數就等於 channel 個數* 4 。

CNN 裏面有 5 個批量歸一層，每層裏面移動均值和移動標准差只用計算而不需要訓練，因此非訓練參數為 32* 2 + 32* 2 + 64* 2 + 64* 2 + 128* 2 = 640 個。

3.6 訓練評估

萬事俱備，只欠訓練。這一次我們增加了參數 validation_data，用於監控模型在訓練時是否出現過擬合，而過擬合發生在訓練誤差 (loss) 一直在減小，但是驗證誤差 (val_loss) 卻在增加。從下圖看還沒出現這樣的問題。

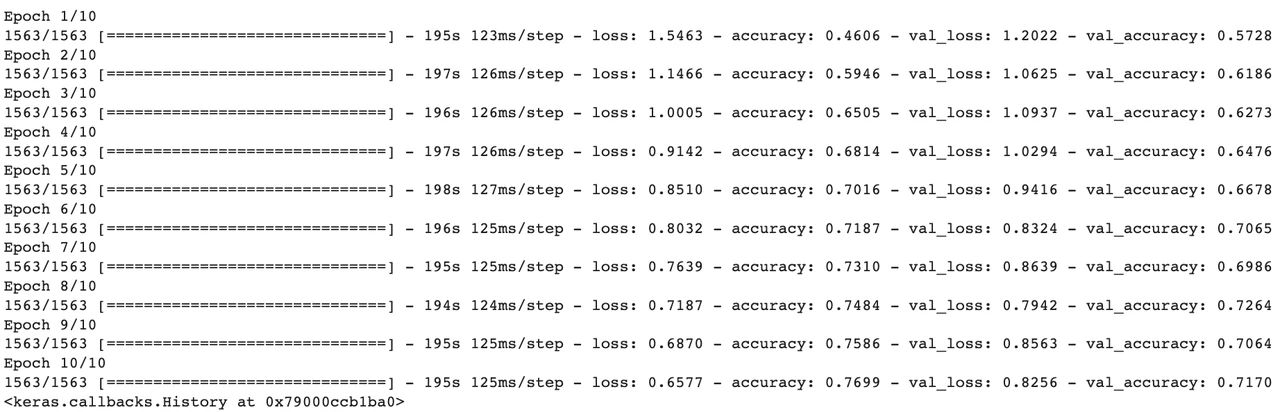
對比現在的卷積神經網絡 (CNN) 和之前的前饋神經網絡 (FNN)，現有模型在訓練集的准確率從之前 51.39% 提升到 76.99% ，在訓練集的准確率也從之前 49.52% 提升到 71.70% ，模型性能大大提高。

神奇的是，CNN 的參數 ( 592, 554) 其實比 FNN 的參數 ( 646, 260) 少很多，但模型性能卻提高了不少，而這種提升只需更改模型架構以包括卷積層、批量歸一層和失活層即可實現。 雖然 CNN 比 FNN 的參數少，但是層數確多很多，這就是為什么深度神經網絡的優勢，因為網絡的中間層捕獲了我們最感興趣的高級特徵 (high-level features)。

從上面 10 張小圖可看出，模型預測正確了 6 張，正確率 60% ，雖然之前統計出來的 71.70% 低，但這個是從 10000 張測試集中採樣出來的 10 張，因此看到模型正確預判了 6, 7, 8 張都是正常的。

總結

本篇介紹了开始構建深度生成模型所需的核心深度學習概念。使用 Keras 構建前饋神經網絡 (FNN)，並訓練模型來預測 CIFAR-10 數據集中給定圖像的類別。 然後，我們通過引入卷積層、批量歸一層和失活層來改進此架構，以創建卷積神經網絡 (CNN)。

深度神經網絡在設計上是完全靈活的，盡量有最佳實踐，但我們可隨意嘗試不同的層以及其出現的順序，用 Keras 實現就像拼樂高積木一樣絲滑，你的神經網絡的設計僅受你自己的想象力的限制。

下篇我們將使用這些模塊來設計一個可以生成圖像的網絡。生成式 AI 的好戲剛剛开始！

您可在 ChatGPT 4.0 的 Plugin Store 搜索 SignalPlus ，獲取實時加密資訊。如果想即時收到我們的更新，歡迎關注我們的推特账號@SignalPlus_Web 3 ，或者加入我們的微信群（添加小助手微信：chillywzq）、Telegram 群以及 Discord 社群，和更多朋友一起交流互動。

SignalPlus Official Website: https://www.signalplus.com

鄭重聲明：本文版權歸原作者所有，轉載文章僅為傳播信息之目的，不構成任何投資建議，如有侵權行為，請第一時間聯絡我們修改或刪除，多謝。