初探全同態加密之二：格密碼學與LWE問題

2023-10-09 16:10:50

作者：Steven Yue，原刊於作者知乎

上一期文章中，我們一起學習了全同態加密（FHE）的定義和具體的幾個階段，並且也回顧了FHE的歷史。到這裏，大家應該對FHE系統已經有一個比較初步的了解了。（可點擊《初探全同態加密：FHE的定義與歷史回顧》查看原文）

我們在上一篇文章的結尾提到了GSW系統，也就是我們所說的第三代全同態加密系統。GSW系統的構造主要是基於格密碼學中有名的LWE問題假設。為了更加方便與我們來了解GSW系統的具體構造，我們這期文章來快速地學習一下，格密碼學與LWE問題究竟是什么。

格密碼學（Lattice-based Crypto）是現在比較火的一個密碼學分支，而且本身擁有抵抗量子計算的特性。在即將到來的NIST後量子時代加密算法標准化討論中，基於格的加密體系就是其中的一個選擇之一。不過大家不要被這些定義嚇到了，其實想要理解格密碼學非常簡單，我們只需要一些最基本的线性代數知識。

PS：如果對线性代數內容比較生疏的話，筆者強烈建議去看3Blue1Brown大神的視頻合集线性代數的本質。視頻裏面非常生動的描述了线性代數的基本定理。

格密碼學快速入門

到底什么是格密碼學？聽了半天想必大家還沒搞明白，其實格密碼學就是基於格（Lattice）和格上的一些問題而定義的一套密碼學體系。所以我們需要先搞明白，格到底是什么。

為了更加方便的舉例子，我們這裏介紹一個最簡單的格系統——整數格（Integer Lattice）。

整數格（Integer Lattice）的構造

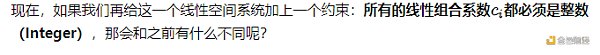
PS：格密碼學中還有另一個難題叫SVP問題（Shortest Vector Problem），和CVP不同，但也是NP-hard的問題。我們在這裏就不多解釋了。

Learning With Error（LWE）問題

讀到這裏，想必大家應該對整數格已經有了一個大致的理解，並且也知道了整數格中的一個難問題：CVP問題。現在我們一起來看看，如何從CVP問題出發，衍生到我們的主角LWE問題上。為了更加方便理解LWE，我們不妨先來回顧一下中學數學～

我們在初中或者高中的數學課上應該都學過如何求解线性方程組（solve system of equations）。一般來說，我們會給到一組多元一次方程：

有噪音的高斯消除問題（Gaussian Elimination with Noise）

當我們學會如何求解线性方程組之後，我們發現這其實並不是什么難的問題，只需要不停地在行與行之間相互使用高斯消除，就可以得到未知數的解。畢竟這也是中學的時候學的數學題，難不到哪裏去。

現在，我們把這個高斯消除問題變化一下，給它增加一些難度：增加噪音。

Diffie-Hellman公鑰交換中的離散對數問題（Dlog Problem）

看到這裏，對密碼學熟悉的朋友們可能會對一個問題的多種版本（如搜索、決策）等等並不陌生。沒錯，在我們學習Diffie-Hellman公鑰交換問題的時候，我們也使用了相同的問題轉換。如果不了解的朋友也不用着急，容我解釋一波。

DLWE與DDH的困難度比較

為什么我們要長篇大論的扯DDH問題呢？這是因為，了解了SLWE/DLWE與CDH/DDH這兩對密碼學中被認為困難的問題之後，我們可以來比較他們的困難度分布到底是怎么樣的。

DDH假設其實非常的不完美，甚至於令人頭疼。因為Pairing這個後門的存在，這直接給DDH問題設置了一個驚人的困難度下限——在Pairing存在的組中，DDH問題太簡單了。所以我們在挑選群的時候，一定要精心挑選。DDH的大哥CDH卻不一樣，因為沒有任何高效率的算法可以破解離散對數，所以在任何循環群中的復雜度都較為平均。這樣一來，CDH就算再困難，對於DDH的困難度分布也沒有太多實質性的幫助。我們往往需要使用平均困難度來定義DDH問題的困難度（因為下限太低了）。這在密碼學中是一件非常膈應人的事情，就像是我送給你一輛車，但是告訴你這個車，有一定的可能性會一开就自動散架一樣。

相比起來，LWE問題就完美許多。因為沒有任何像Pairing一樣的後門的存在，所以DLWE問題其實和SLWE的困難度是相同的。因為不管是解決DLWE還是SLWE，我們都會被卡在如何還原未知向量S這一步上面。像這一類就算問題形式被轉換，但是復雜度保證大致相同的問題，在密碼學中是不可多得的寶貝。對於DLWE問題的困難度，我們可以很優雅的使用最壞困難度（Worst Case Performance）來定義。

這一段其實多少都是密碼學界大家的情懷，有一個幹淨的定義比搞一堆亂七八糟的假設來的舒服多了。這也就是為什么格密碼學那么的吸引人的原因。不過，這些關於困難度/復雜度的小情緒，對於我們理解全同態加密是無關緊要的。大家可以當作茶余飯後的趣聞，隨便看看。

DLWE的實战應用：格密碼學與Regev加密算法

如果你成功的啃完了前面的幹貨，看到了這裏，那么恭喜你，現在你已經掌握了LWE與格密碼學的基礎了！

現在，當我們學會了這么多知識之後，我們可以結合一下之前學習的內容，融會貫通一下，來看看如何使用LWE問題來構建一個格密碼學中常見的公鑰加密系統——Regev加密算法。

Regev加密是一個叫Regev的大佬在2005年發明出來的，是一個非常類似於ElGamal類型的公鑰加密系統，基於了DLWE的假設。我們來看看它的具體定義吧：

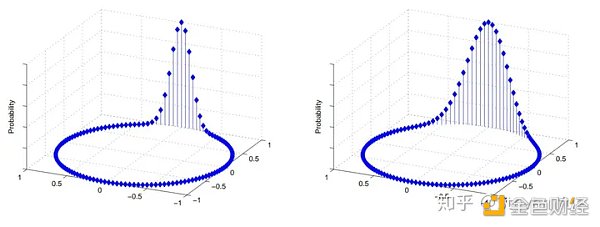
Regev加密的安全性

剛才屬性的話題討論到一半，我們打了個岔。最後我們回來繼續學習一下，Regev加密系統的安全性（Security）。

為了證明Regev加密體系是語義安全的，我們需要使用密碼學中的一種常見的證明工具：混合論證法（Hybrid Argument）。混合論證其實並不是什么黑科技，而是我們把要證明的問題劃分成若幹小步，然後逐步證明罷了。

首先，我們來看一下，假如一個第三方偷看到了Regev加密系統的加密密文的所有消息，那么他的世界觀是這樣的：

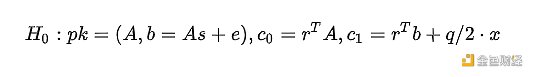
接着，我們可以創建第二個相似的世界觀：

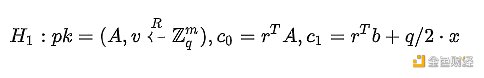
未完待續：構建有限級數全同態算法

最後，我們來回顧一下這一期的內容～

首先，我們一起看到了整數格（Integer Lattice）的定義，然後基於整數格了解了NP-hard的最近向量問題（ CVP）。隨後，我們重新回顧了高中時期學習的求解线性方程組問題，並且統一歸納為高斯消除問題。隨後，我們給高斯消除問題本身加入了一個隨機的誤差噪音，從而構成了我們的主角，誤差還原（LWE）問題。

了解了LWE是什么之後，我們又詳細學習了LWE問題的正式定義，以及其中的n，m，q，B參數。接着我們把搜索LWE（SLWE）轉換為決策LWE（DLWE）問題，然後探討了SLWE/DLWE的假設為什么比CDH/DDH更好。最後，我們結合了所有學習的知識，一起構建了格密碼學中很經典的Regev加密算法，通過LWE的困難假設對密文（一個bit）進行加密。

如果你讀到這裏，並且成功的理解了所有的內容的話，那么其實你已經掌握了全同態加密80%的精髓了！接下來，我們需要做的只是把這些部分像搭積木一樣搭起來，就可以構成我們想要的全同態加密系統了。

由於篇幅原因，我們這一期就寫到這裏。下一期，我們使用這期學到的知識，一起來構建一個有限級數全同態加密體系。