Gate Ventures研究院：FHE，披上哈利波特的隱身衣

2024-09-29 00:09:07

什么是 FHE

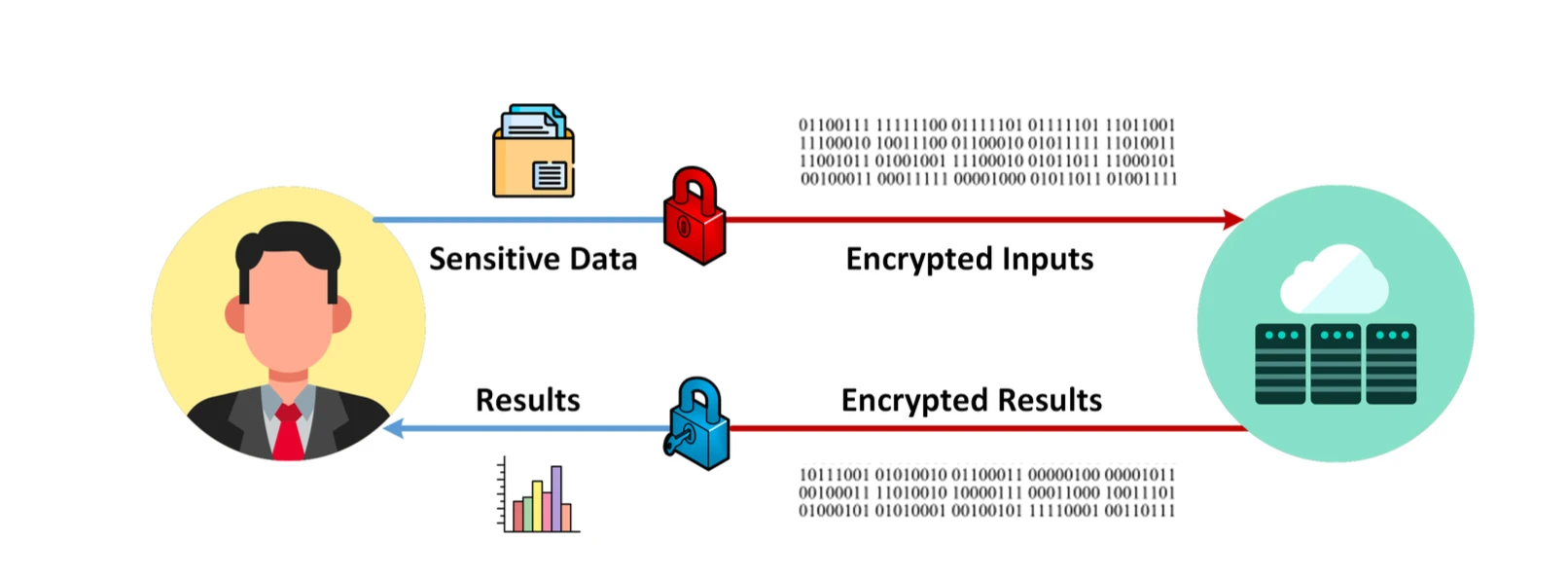
FHE 流程，圖源：Data Privacy Made Easy

FHE（Fully homomorphic encryption）是一項先進的加密技術，可以支持在加密的數據上進行直接計算。這意味着可以在保護隱私的同時對數據進行處理。FHE 有多個可落地的場景，特別是在隱私保護下的數據處理與分析，如金融、醫療健康、雲計算、機器學習、投票系統、物聯網、區塊鏈隱私保護等領域。但是商業化仍然需要一定的時間，主要問題在於其算法帶來的計算與內存开銷極為龐大，可拓展性較差。接下來我們將簡要 walk through 整個算法基本原理以及着重講述該密碼學算法面臨的問題。

基本原理

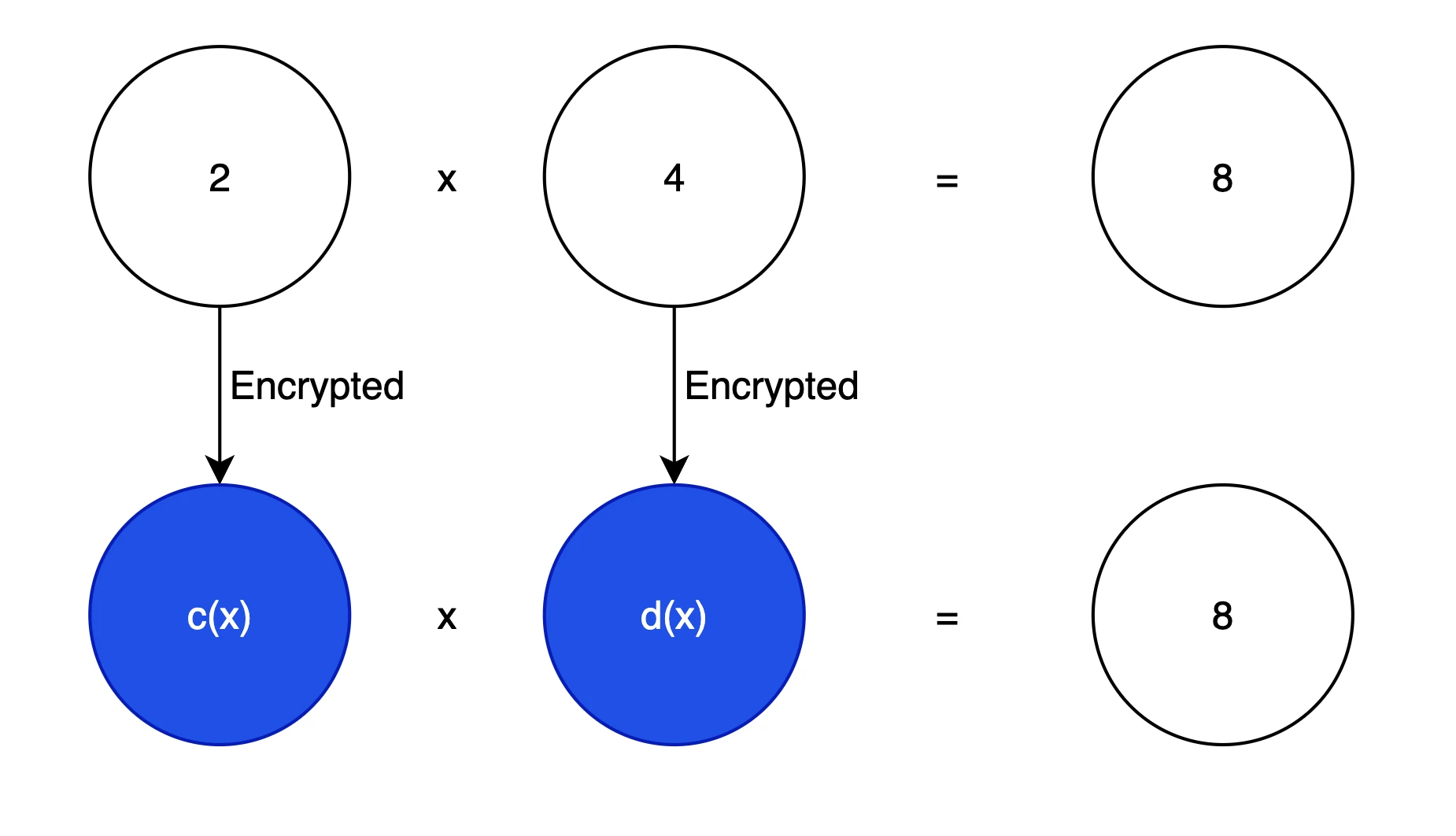
同態加密圖示

首先，我們要實現加密的數據進行計算然後還能得到相同的結果，我們可視化如上圖所示。這是我們的基本目標。在密碼學中，通常使用多項式，來隱藏原文的信息，因為多項式能夠轉換為线性代數的問題，也可以轉換為向量的計算問題，這便於為向量進行高度優化的現代計算機進行運算（如並行計算），例如， 3 x 2 + 2 x + 1 可以表示為向量 [ 1, 2, 3 ]。

假設，我們要加密 2 ，在一個簡化的 HE 系統中，我們可能會：

選擇一個密鑰多項式，比如 s(x) = 3 x 2 + 2 x + 1
生成一個隨機多項式，比如 a(x) = 2 x 2 + 5 x + 3
生成一個小的“錯誤”多項式，比如 e(x) = -1 x + 2
加密 2 -> c(x) = 2 + a(x)*s(x) + e(x)

我們講一下為什么需要這樣做，我們現在假設拿到了密文 c(x)，如果想要得到明文 m，則公式為 c(x) - e(x) - a(x)*s(x) = 2 ，這裏我們隨機多項式假設 a(x)是公开的，那么只要保證我們的密鑰 s(x)是保密的即可，我們如果知道了 s(x)，再加上 c(x)作為一個很小的誤差，那么理論上可以忽略，就能得到明文 m。

這裏有第一個問題，多項式那么多，如何選擇多項式呢？多項式的度多大比較好呢？實際上多項式的度是由實現 HE 的算法決定的。通常是 2 的冪次，如 1024 / 2048 等。多項式的系數由一個有限域 q 中隨機選擇，如 mod 10000 ，則在 0-9999 中隨機選擇，系數隨機選擇有很多算法遵循，如均勻分布、離散高斯分布等等。不同的方案也有不同的系數選擇要求，通常是為了滿足該方案下的快速求解原則。

第二個問題，噪聲是什么？噪聲是用來迷惑攻擊者的，因為假設我們的所有數字都是採用 s(x)，並且隨機多項式處於一個有域中，那么就存在一定的規律，只要輸入足夠多次的明文 m，根據輸出的 c(x)，就能判斷這兩個 s(x)與 c(x)的信息。如果引入了噪聲 e(x)，就能保證無法通過簡單的重復列舉獲得 s(x)與 c(x)，因為這有一個完全隨機的小誤差存在。這個參數也被稱為噪聲預算（Noise Budget）。假設 q = 2 ^ 32 ，初始噪聲可能在 2 ^ 3 左右。經過一些操作後，噪聲可能增長到 2 ^ 20 。此時仍有足夠空間進行解密，因為 2 ^ 20 << 2 ^ 32 。

我們獲得了多項式以後，我們現在要把 c(x) * d(x)操作轉化為“電路”，這個在 ZKP 中也經常出現，主要是因為電路這個抽象概念提供了一個通用的計算模型表示任何計算，並且電路模型允許精確跟蹤和管理每個操作引入的噪聲，也方便後續引入到專業硬件中如 ASIC、FPGA 進行加速計算，如 SIMD 模型。任何復雜的操作都可以映射成簡單的模塊化的電路元素，如加法和乘法。

算術電路表示

加法和乘法就能夠表達減法以及除法，因此就能夠表達任意計算。多項式的系數用二進制表示，稱為電路的輸入。每個電路的節點代表了執行一次加法或者乘法。每個(*)代表乘法門，每個(+)代表加法門。這個就是算法電路。

這裏就引申出一個問題，我們為了語義信息上不泄漏，因此引入了 e(x)，這被稱為噪聲。我們的計算中，加法會讓兩個 e(x)多項式變成，同度的多項式。在乘法中，兩個噪聲多項式相乘，會讓 e(x)的度以及文本大小指數級增加，如果噪聲過大，就會導致結果計算的過程中，噪聲無法忽略，進而導致原文 m 無法恢復。這是一個限制 HE 算法表達任意計算的主要原因，因為噪聲會指數級增長，導致很快就達到了不可用的閾值。在電路中，這個被稱為電路的深度，乘法運算的次數也就是電路的深度數值。

同態加密 HE 的基本原理如上圖所示，為了解決制約着同態加密的噪聲問題，因此提出了多項解決方案：

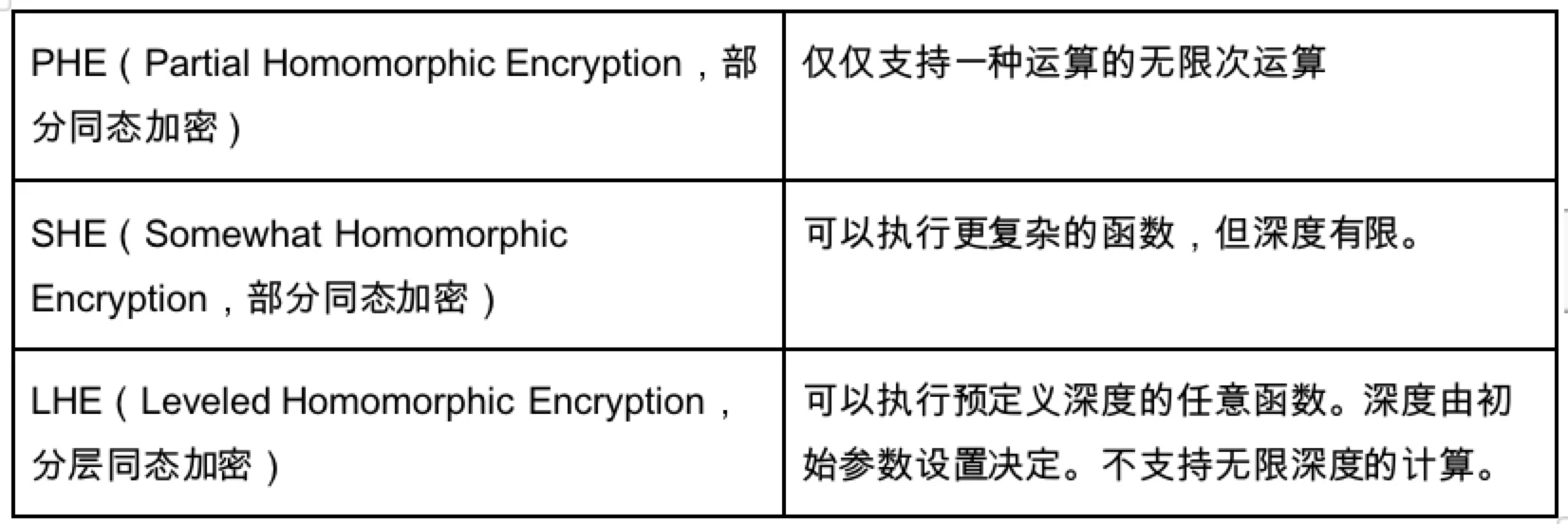
這裏面 LHE 是一個很適合的一個算法，因為在這個算法下，只要深度確定了就能在深度內執行任意函數，但是 PHE 以及 SHE 無法實現圖靈完備。因此在這個基礎上，密碼學家進行研究，提出了三個技術來構建 FHE 全同態加密，期望實現在無限深度執行任意函數的愿景。

Key switching（密鑰切換）：我們在乘法後，密文的大小會指數級增長，這會讓後續的操作內存和計算資源提出極大的要求，因此在每次乘法後實施 Key switching 就能壓縮密文，但是會引入一點噪聲。
Modulus Switching（模數切換）：無論是乘法還是 key switching 都會讓噪聲指數級增加，模數 q 是我們前面講過的 Mod 10000 ，只能在[ 0, 9999 ]裏面取參數，q 越大則噪聲經過多次計算後最後噪聲仍然在 q 內，則可以解密。因此在多次操作後，為了避免噪聲指數級增大超過閾值，那么就需要使用 Modulus Switching，來減小噪聲預算，這樣就可以壓低噪聲。我們這裏就可以得到一個基本的原理，如果我們的計算很復雜，電路深度很大，那么就需要更大的模數 q 噪聲預算來容納多次指數級增長後的可用性。
Bootstrap：但是想要實現無限深度的計算，Modulus 只能限制噪聲的增長，但是每次切換都會讓 q 範圍變小，我們知道一旦減小，意味着計算的復雜度就需要降低。Bootstrap 是一項刷新技術，就是將噪聲重置到原始水平，而不是減小噪聲，bootstrap 不需要減小模數，因此可以維持系統的計算能力。但是其弊端就是需要消耗大量的算力資源。

總的來說，針對有限步驟下的計算，使用 Modulus Switching 能夠降低噪聲，但是同時也會降低模數，也就是噪聲預算，導致壓縮計算能力。因此這僅僅針對有限步驟下的計算。對於 Bootstrap 能夠實現噪聲重置，因此在基於 LHE 算法之上，能夠實現真正意義上的 FHE，也就是任意函數的無限計算，而這也是 FHE 的 Fully 的含義。

但是缺點也很明顯就是需要消耗大量的算力資源，因此一般情況下，這兩種降噪技術會結合使用，Modulus switching 用於日常的噪聲管理，延遲需要 bootstrap 的時間。當 modulus switching 無法進一步有效控制噪聲時，才使用計算成本更高的 bootstrap。

目前 FHE 的方案有以下具體的實現，都使用的 Bootstrap 核心技術：

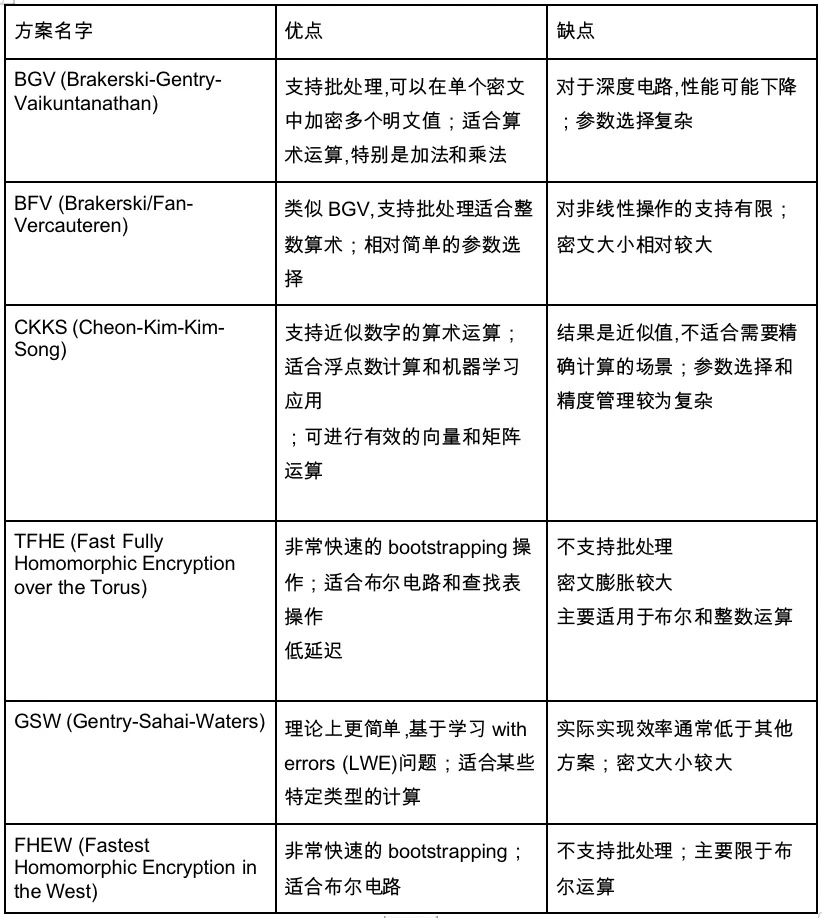
這裏也就引出了我們一直未談及的電路類型，在上面我們介紹的主要是算術電路。但是還有另外一個電路類型——布爾電路。算術電路是 1+ 1 這種比較抽象的，節點也是加法或者除法，而布爾電路所有的數字轉化為 01 進制，所有的節點是 bool 運算，包括 NOT、OR、AND 運算，類似於我們的計算機的電路實現。而算術電路更是一個抽象上的電路。

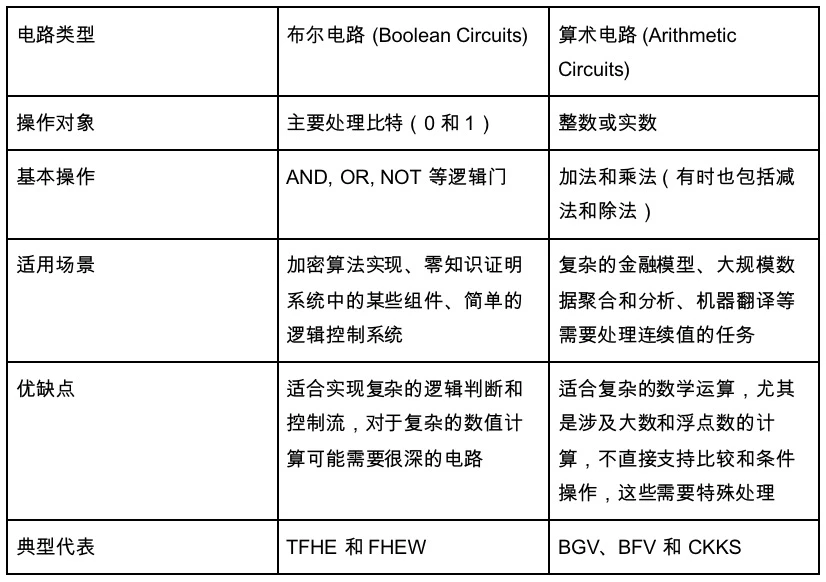
因此，我們可以非常粗略的將布爾運算視為沒有那么數據密集的靈活的處理，而算術運算是針對數據密集型應用的方案。

FHE 面臨的問題

由於我們的計算需要加密然後轉換為“電路”，並且由於單純的計算僅僅計算 2+ 4 ，但是在加密後，引入了大量的密碼學間接的計算過程，以及一些前沿技術如 Bootstrap 來解決噪聲問題，進而導致了其計算开銷是普通計算的 N 個數量級。

我們以一個現實世界的列子來讓讀者感受這些額外的密碼學過程對計算資源的开銷。假設普通計算在一個 3 GHz 的處理器上需要 200 個時鐘周期,那么一次普通的 AES-128 解密大約需要 67 納秒( 200/3 GHz)。FHE 版本需要 35 秒,是普通版本的大約 522, 388, 060 倍( 35/67 e-9)。也就是，使用相同的計算資源，同一個普通算法和 FHE 計算下的算法，其對計算資源的要求大概是 5 億倍。

DARPA dprive 計劃，圖源： DARPA

美國的 DARPA 為了數據安全，因此在 2021 年專門構建了一個 Dprive 計劃，邀請了多個研究團隊包括微軟、Intel 等，他們的目標是創建一個 FHE 加速器以及配套的軟件堆棧，使 FHE 計算速度更符合未加密數據的類似操作，實現 FHE 計算速度大約為普通計算的 1/10 的目標。DARPA 項目經理 Tom Rondeau 指出：“估計，在 FHE 世界中，我們的計算速度比在純文本世界中慢大約一百萬倍。

而 Dprive 主要從以下幾個方面着手：

增大處理器字長：現代計算機系統使用 64 位的字長，也就是一個數字最多 64 位，但是實際上 q 往往 1024 位，如果想要實現就要拆分我們的 q，這樣會對內存資源和速度有損耗。因此為了實現更大的 q，需要構建一個 1024 位或者更大字長的處理器。有限域 q 非常重要，就像我們前面提到的，越大，那么可計算的步驟就越多，對於 bootstrap 的操作就可以盡可能的往後推遲，這樣整體的計算資源消耗就會減小。q 在 FHE 中扮演着核心角色，它影響了方案的幾乎所有方面，包括安全性、性能、能夠進行的計算量以及所需的內存資源。

構建一個 ASIC 處理器：我們前面講到過由於便於並行化以及其它原因，我們構建了多項式，通過多項式構建了電路，這個和 ZK 是相似的。目前的 CPU、GPU 不具備這個能力（算力資源以及內存資源）來運行電路，需要構建專門的 ASIC 處理器來允許 FHE 算法。

構建並行化架構 MIMD，與 SIMD 並行架構不同，SIMD 只能在多個數據上執行單一指令，也就是數據的拆分與並行處理，但是 MIMD 可以拆分數據使用不同的指令進行計算。SIMD 主要用於數據並行，這也是大多數區塊鏈項目對交易並行處理的主要架構。而 MIMD 能夠處理各種類型的並行任務。MIMD 在技術上更復雜，需要着重處理同步與通信問題。

距離 DARPA 的 DEPRIVE 計劃僅僅剩下一個月的時間就到期了，原本計劃 Dprvie 是從 2021 年开始， 2024 年 9 月份三個階段的計劃結束，但是似乎其進展緩慢，目前仍然未達到預期的相比於普通計算 1/10 效率的目標。

雖然攻破 FHE 技術進展緩慢，類似於 ZK 技術一樣，面臨這硬件落地是技術落地的前提這一嚴峻問題。但是，我們仍然認為從長期來看，FHE 技術仍然有其獨特的意義，特別是我們第一部分羅列的保護部分安全數據的隱私上。對於 DARPA 國防部來說，其掌握了大量的敏感數據，如果想要將 AI 泛型能力釋放到軍事上，就需要以數據安全的形式訓練 AI。不僅如此，對於醫療、金融等關鍵敏感數據也同樣適用，實際上 FHE 並不適用於所有的普通計算，更加面向於敏感數據下的計算需求，這種安全性對於後量子時代尤為重要。

對於這種前沿技術，必須要考慮投資周期與商業化落地的時間差。因此，我們需要非常謹慎的看待 FHE 的落地時間。

區塊鏈的結合

在區塊鏈中，FHE 也主要用於保護數據的私密性，應用領域包括鏈上隱私、AI 訓練數據的隱私、鏈上投票隱私、鏈上隱私交易審查等方向。其中 FHE 也被稱作鏈上 MEV 方案的潛在解決方向之一。根據我們的 MEV 的文章《照亮黑暗森林 — 揭开 MEV 神祕面紗》所述，當前的許多 MEV 方案僅僅是重新構建 MEV 架構的方式，並不是解決的方式，實際上三明治攻擊帶來的 UX 問題仍然沒有解決。我們一开始想到的方案也是，直接對交易加密，同時保持狀態的公开。

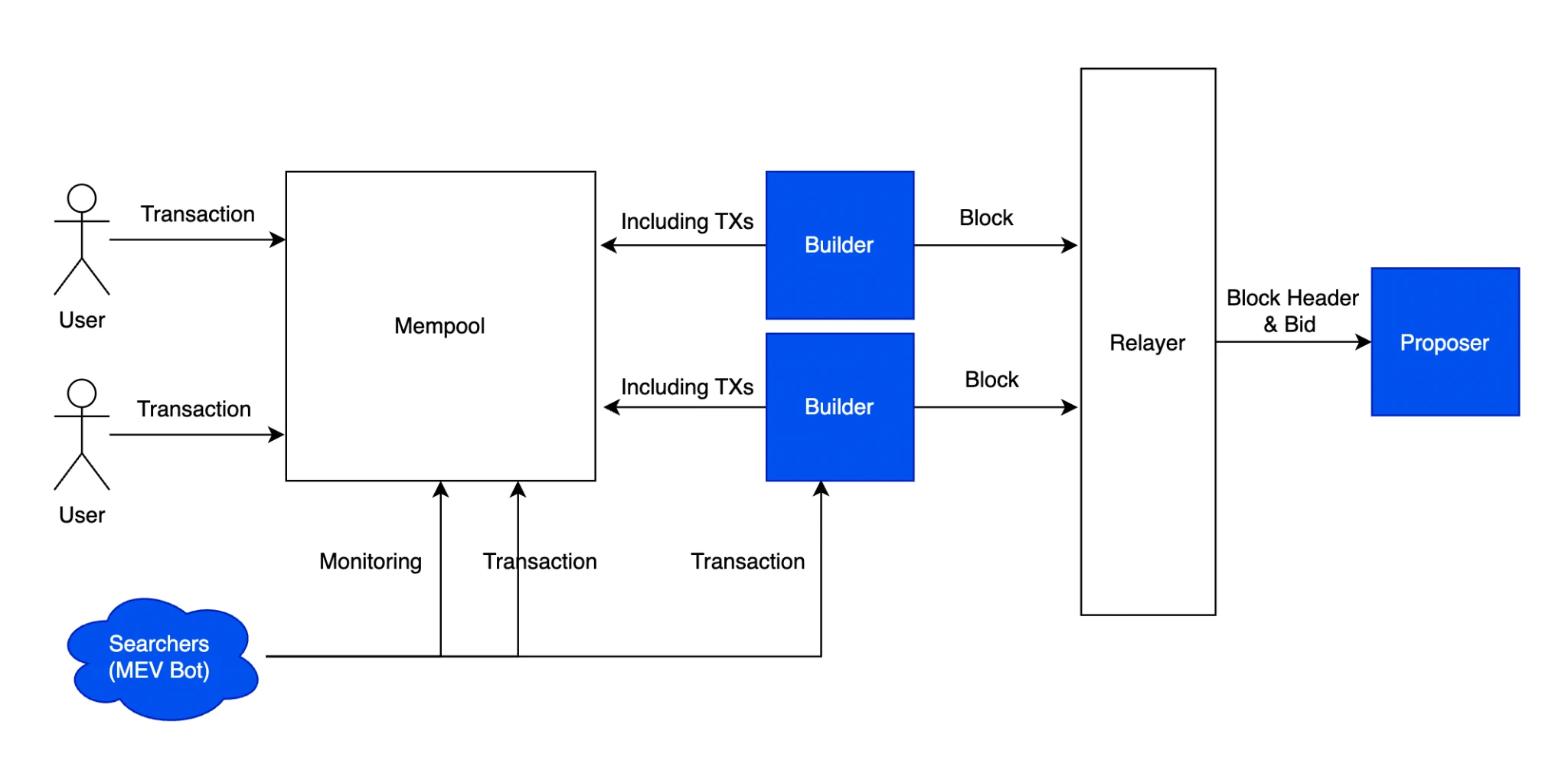
MEV PBS 流程

但是也有一個問題就是如果我們對交易進行完全的加密，就會讓 MEV bots 帶來的正外部性也同時消失，驗證者 Builder 需要運行在虛擬機的基礎上進行 FHE，驗證者也需要驗證交易以確定最後的狀態正確性，那么就會顯著提高運行節點的要求，讓整個網絡的吞吐量放慢百萬倍。

主要項目

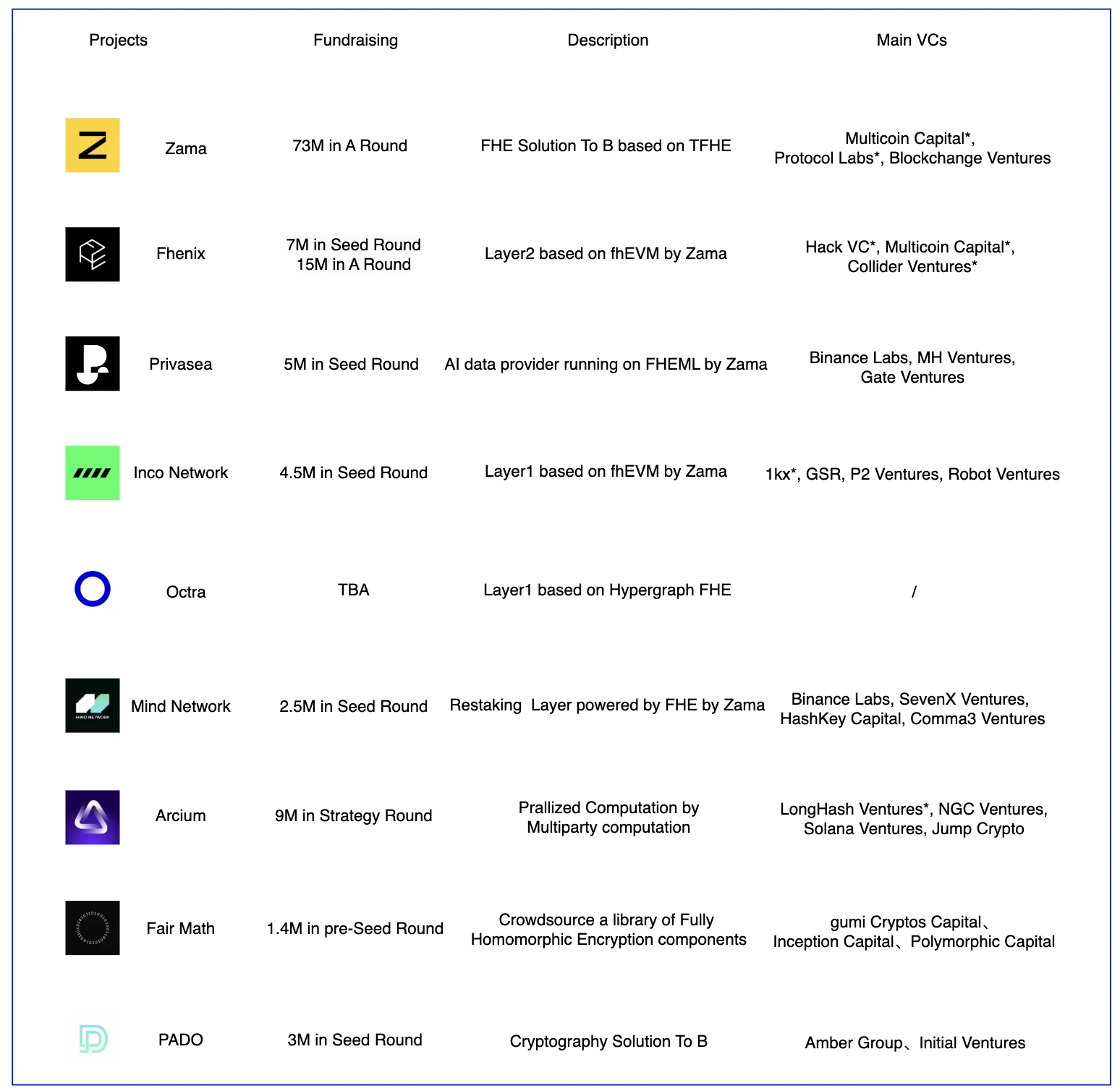
FHE Landscape

FHE 是一項較新的技術，目前大部分的項目使用的 FHE 技術都來自於 Zama 構建的，如 Fhenix、Privasea、Inco Network、Mind Network。Zama 的 FHE 工程實現能力獲得了這些項目的認可。以上幾個項目大部分都基於 Zama 提供的庫進行構建，主要區別在於商業模式。Fhenix 希望構建一個隱私優先的 Optimism Layer 2 ，Privasea 希望運用 FHE 的能力來進行 LLM 的數據運算，但是這是一項非常重數據的操作，對 FHE 的技術與硬件要求都特別高，然後 Zama 基於的 TFHE 可能不是最優的選擇。Inco Network 與 Fhenix 都使用 fhEVM，但是一個是構建 Layer 1 一個是 Layer 2 。Arcium 是構建了多種密碼學技術的融合，包括了 FHE、MPC 和 ZK。Mind Network 的商業模式比較另闢蹊徑，選擇了 Restaking 賽道，通過提供流動安全性和基於 FHE 的子網架構來解決共識層的經濟安全與投票信任的問題。

Zama

Zama 是基於 TFHE 的方案，其特點是使用了 Bootstrap 技術，其着重於處理布爾運算和低字長的整數運算，雖然在我們實現了 FHE 的方案中是一個較快的技術實現，但是其相比與普通計算仍然有非常大的差距，其次也無法去實現任意計算，在面對數據密集型的任務時，這些運算會導致電路的深度過大而無法處理。其不是數據密集型的方案，其只適用於某些關鍵步驟的加密處理。

TFHE 目前已經有了現成的實現代碼，Zama 的主要工作是使用 Rust 語言重寫了 TFHE，也就是其 rs-TFHE crates。同時為了降低用戶使用 Rust 的門檻，其也構建了一個轉編譯的工具 Concrate，能夠把 Python 轉化為 rs-TFHE 等效的。使用這個工具，就能把基於的 Python 的大模型語言轉譯到基於 TFHE-rs 的 rust 語言。這樣就能運行基於同態加密的大模型，但是這時數據密集型的任務，其實並不適合 TFHE 的場景。Zama 的產品 fhEVM 是一種使用完全同態加密（FHE）在 EVM 上實現機密智能合約的技術，能夠支持基於 Solidity 語言編譯端到端加密的智能合約。

總的來說，Zama 作為一個 To B 的產品，其構建了較為完善的基於 TFHE 的區塊鏈+AI 开發堆棧。能夠幫助web3的項目簡單的構建 FHE 的基礎設施和應用。

Octra

Octra 比較特殊的一點是，使用了另闢蹊徑的技術來實現 FHE。其使用了一個稱為 hypergraphs 的技術來實現 bootstrap。也是基於布爾電路，但是 Octra 認為基於 hypergraphs 的技術，能實現更高效的 FHE。這個是 Octra 實現 FHE 的原創技術，團隊具備非常強的工程、密碼學能力。

Octra 構建了新的智能合約語言，其使用 OCaml、AST、ReasonML（一種專門用於與 Octra 區塊鏈網絡交互的智能合約和應用程序的語言）等代碼庫和 C++ 進行开發。其構建的 Hyperghraph FHE 庫，能夠與任何項目兼容。

其架構也是類似於 Mind Network、Bittensor、Allora 等項目，其構建了一個主網，然後其它項目成為 subnets，構建了一個相互隔離的運行環境。同時，與這些項目類似，都構建了更適合架構本身的新興共識協議，Octra 構建了一個基於機器學習的共識協議 ML-consensus，其本質是基於 DAG（有向無環圖）的。

該共識的技術原理目前還未披露，但是我們可以大致的推測。大概就是交易被提交到網絡中，然後使用 SVM（支持向量機）算法來決定最佳的處理節點，主要是通過目前各個節點的網絡負載情況選擇。系統會基於歷史數據（ML 算法學習）來判斷最好的父節點共識達成的路徑。只要滿足 1/2 的節點就可以達成該不斷增長的數據庫的共識。

期待

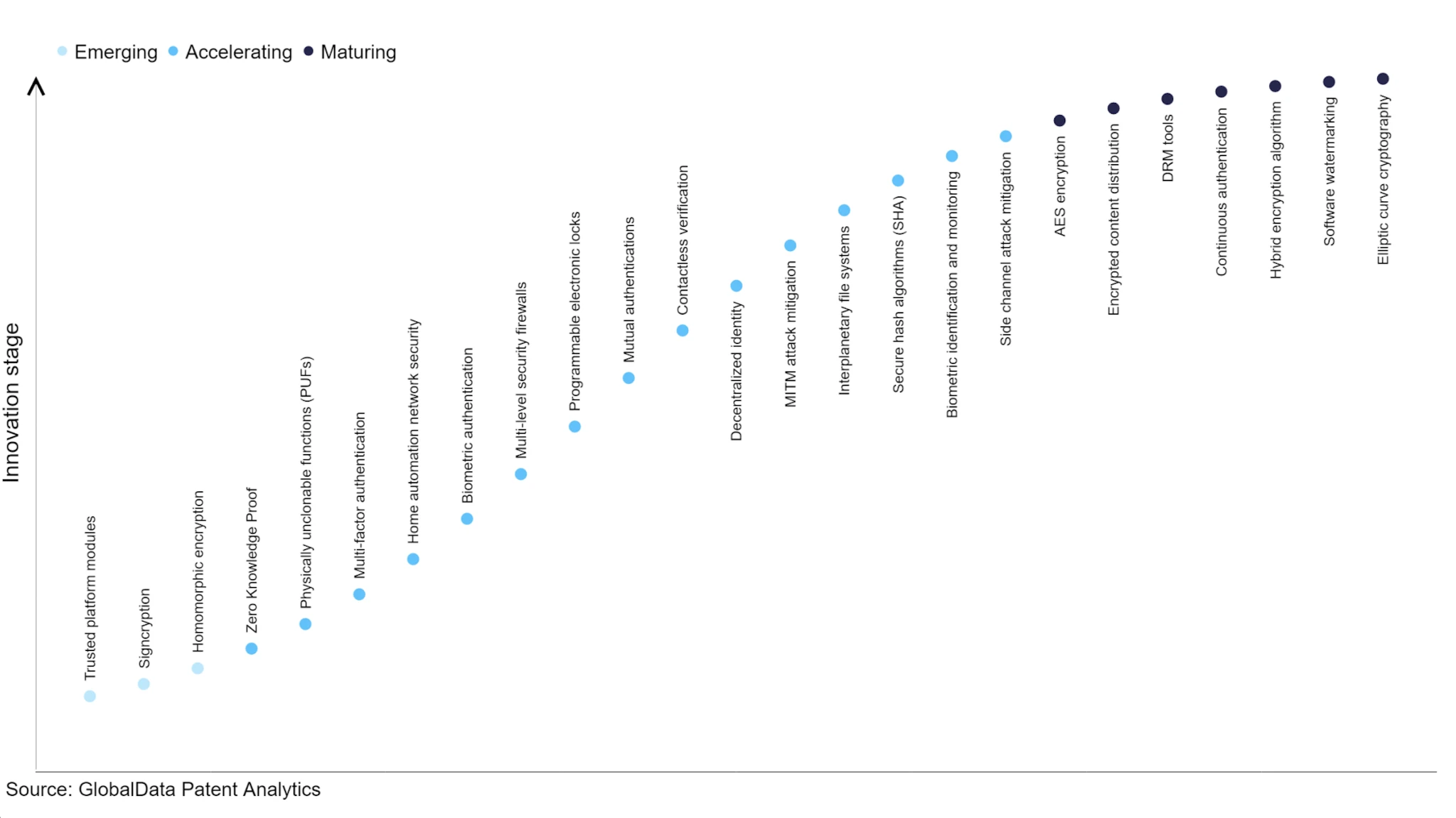
前沿密碼學技術發展現狀，圖源： Verdict

FHE 技術是一種面向於未來的技術，其發展現狀仍然不及 ZK 技術，缺乏資本的投入，因為隱私保護帶來的低效率以及高成本對大部分商業機構來來說都動力不足。ZK 技術的發展因為 Crypto VC 的投入變得更加快速。FHE 仍然處於非常早期，即使是現在，市面上的項目仍然較少，因為其成本高昂、工程難度高、商業化落地前景仍然不明朗的等原因導致。2021 年 DAPRA 聯合多家公司如 Intel、Microsoft 等开啓了長達 42 個月的 FHE 攻克計劃，雖然取得一定進展，但是距離實現的性能目標仍然較遠。隨着 Crypto VC 對該方向的注意力到來，會有更多的資金湧入這個行業，預計業內會有更多的 FHE 項目出現，也會有更多類似 Zama、Octra 等具備很強工程與研究能力的團隊站在舞臺中央，FHE 技術對於區塊鏈的商業化和發展現狀的結合仍然值得探索，目前應用較好的就是驗證節點投票的匿名化，但是應用範圍仍然狹小。

與 ZK 一樣，FHE 芯片的落地是 FHE 商業化落地前提條件之一，目前有多個廠商如 Intel、Chain Reaction、Optalysys 等在探索這一方面。即使 FHE 面臨許多的技術阻力，但是伴隨着 FHE 芯片的落地，全同態加密作為一項極具前景和確切需求的技術，其對於如國防、金融、醫療等行業會帶來深刻的變革，釋放這些隱私數據與未來量子算法等技術結合的潛力，也會迎來其爆發時刻。

我們愿意探索這一早期的前沿技術，如果你正在構建真正得以商業化落地的 FHE 產品，或者有更具前沿眼光的技術創新，歡迎與我們接觸！