B² Network技術實現：基於零知識證明驗證承諾的比特幣ZK-Rollup

原文作者： Stone , B² Network Research Lead

B² Network 是比特幣上的一個 Layer 2 解決方案，主要利用將零知識證明驗證承諾提交到比特幣網絡，允許挑战者發起欺詐證明進行挑战，以達到利用比特幣網絡的強大共識保證 B² Network 安全性的目的。

本文主要介紹以太坊上的 ZK-Rollup 和 OP-Rollup 的運行機制，介紹神奇的與非門電路，介紹承諾的作用，並利用這些機制和概念設計 B² Network 上的零知識證明驗證承諾，進而說明零知識證明驗證承諾如何在比特幣網絡執行以及如何保證 B² Network 的安全性。

以太坊上的 ZK-Rollup

ZK-Rollup 是一種區塊鏈的二層擴展解決方案，通過聚合多個交易並利用零知識證明來確保這些交易批次的正確性和完整性，並在一層區塊鏈網絡上進行零知識證明的驗證，從而利用一層網絡保證二層網絡的安全性。它旨在提高區塊鏈系統的吞吐量，減少交易費用，同時保持高度的安全性和數據完整性。

ZK-Rollup 的運行過程大致如下：

1. 交易聚合和排序。用戶向 ZK-Rollup 提交交易，交易將會被提交到 mempool 中。ZK-Rollup 的 Sequencer 從 mempool 中獲取用戶的交易並進行收集、排序，Sequencer 負責處理交易，更新账戶狀態，並最終生成一個代表這些更新的批次；

2. 狀態轉換和計算。所有的交易執行和狀態更新都在鏈下進行。ZK-Rollup 的 VM（包括 zkEVM、zkVM 等不同的零知識證明智能合約執行引擎）計算新的账戶狀態，並處理如轉账、智能合約交互等操作。同時生成必要的數據和證據來證明這些交易和狀態更新是有效的，這裏面包括新的账戶狀態和零知識證明；

3. 零知識證明生成。ZK-Rollup 的 Prover 利用零知識證明技術（如 zk-SNARKs 或 zk-STARKs）來創建一個證明，這個證明表明所有聚合的交易都是有效的，沒有違反網絡規則。這個證明不透露任何有關交易內容的信息，保護用戶隱私，同時確保了數據的完整性和安全性。

4. 零知識證明驗證。Aggregator 將批次的數據和零知識證明提交到一層區塊鏈網絡。這通常以一種壓縮的形式發生，以減少所需的鏈上空間。一層區塊鏈網絡上的智能合約接收這些數據和證明，並驗證證明的有效性。如果證明有效，合約將更新其記錄的 ZK-Rollup 層的狀態。

ZK-Rollup 的核心在於零知識證明的生成和驗證。ZK-Rollup 的交易在鏈下執行，並在鏈下生成狀態，通過 Prover 生成零知識證明，作為 ZK-Rollup 的承諾。這個承諾代表着 ZK-Rollup 上的交易正確、有效地執行，生成了正確的狀態。一層區塊鏈網絡不需要驗證 ZK-Rollup 的全部交易和狀態，只需要驗證承諾，承諾的驗證是通過一層網絡的智能合約進行零知識證明驗證，即可確認 ZK-Rollup 的有效性。

因此，在以太坊的 ZK-Rollup 中，零知識證明數據是二層網絡向一層網絡提交的承諾。

以太坊上的 OP-Rollup

Optimistic Rollup (OP-Rollup) 是一種為了擴展區塊鏈性能而設計的技術，它通過在鏈上保持最小的數據和執行盡可能多的計算在鏈下來實現。OP-Rollup 利用了“樂觀”假設，即大部分交易都是誠實的，而不是立即驗證每個交易的有效性，這樣可以在一段時間後再進行驗證，極大地提高了吞吐量和效率。

OP-Rollup 的運行過程大致如下：

1. 交易聚合和排序。用戶向 OP-Rollup 提交交易，交易將會被提交到 mempool 中。OP-Rollup 的 Sequencer 從 mempool 中獲取用戶的交易並進行收集、排序，Sequencer 負責處理交易，更新账戶狀態，並最終生成一個代表這些更新的批次；

2. 交易的執行。OP-Rollup 的交易在鏈下執行，每個批次交易的執行，將導致舊的狀態轉變為新的狀態，每個批次都會計算一個新的狀態根（一種加密的“快照”表示整個系統狀態），並將其提交到一層區塊鏈網絡；

3. 狀態的驗證。OP-Rollup 在提交交易批次時不立即進行復雜的驗證，而是“樂觀地”假設這些交易都是有效的，然後提交一層區塊鏈網絡。如果有觀察者認為某個批次是無效的，他們可以提交一個欺詐證明來挑战該批次。在 Optimistic Rollup 解決方案中，欺詐證明是一種允許任何觀察者挑战錯誤或惡意提交到鏈上的狀態或交易的機制。Optimistic Rollup 利用欺詐證明來確保即使是“樂觀地”接受的交易也可以在事後被證明是錯誤的，並相應地被撤銷；

4. 挑战機制。挑战期是 OP-Rollup 提交狀態確認後，有一個挑战窗口期，期間任何人都可以檢查提交的批次，並在發現錯誤時提交欺詐證明，這通常是通過提交一個交易到一層區塊鏈網絡來實現，該交易聲明了他們認為的錯誤並提供了相應的證據。 Arbitrum Rollup（一種 Optimistic Rollup 的解決方案）使用一種稱為“交互式驗證遊戲”的過程來解決挑战。在這個過程中，挑战者和提交者之間進行一系列的回合，逐步縮小他們對哪裏出錯的意見不一致的範圍（採用的是二分查找法快速定位錯誤的交易位置）。最終，這個過程將確定錯誤發生的確切位置。一旦錯誤被確認，原始的批次將被撤銷，並對提出錯誤的驗證者進行處罰。如果挑战失敗，則挑战者可能會失去他們為發起挑战而抵押的資金；如果挑战成功，則挑战者可以獲得成功發起挑战贏得的獎勵資金。

OP-Rollup 的核心在於欺詐證明和挑战機制。OP-Rollup 首先會“樂觀”地認為所有交易都正確執行，然後在一層網絡將計算編譯為合約內虛擬機（AVM、OVM）的字節碼，發布字節碼的承諾。OP-Rollup 的承諾驗證，需要進行交易計算，並獲得字節碼，然後驗證承諾。一旦有觀察者發現有承諾不匹配的批次，觀察者將會通過挑战機制生成欺詐證明，獲得獎勵。

以太坊的 OP-Rollup 首先“樂觀”地確認和提交承諾，然後利用挑战機制，允許任何人對提交的承諾進行挑战，最終通過承諾和挑战確保 OP-Rollup 得到驗證和確認。

神奇的與非門

與非門（NAND gate）是數字邏輯中的一種基本邏輯門，它實現了邏輯與（AND）操作後的邏輯非（NOT）操作。與非門的特性使其成為能夠構造任何其他邏輯門和復雜邏輯電路的基礎。以下是如何使用與非門構造邏輯門（如與門、或門、異或門）以及加法門和減法門的詳細介紹：

1. 與非門基礎

與非門有兩個輸入，當且僅當兩個輸入都為 1 時，輸出為 0 ；在所有其他情況下，輸出為 1 。這可以用邏輯表達式表示為 A NAND B。

2. 構造基本邏輯門

與門（AND）

要使用與非門構造與門：

• 第一步：將兩個輸入連接到一個與非門。

• 第二步：將該與非門的輸出連接到另一個與非門的兩個輸入端。

• 結果：第二個與非門的輸出就是與門的結果。

或門（OR）

要使用與非門構造或門：

• 第一步：將每個輸入分別通過一個與非門（自己與自己），產生兩個非門的效果。

• 第二步：將這兩個與非門的輸出作為一個與非門的輸入。

• 結果：該與非門的輸出就是或門的結果。

異或門（XOR）

要使用與非門構造異或門（更復雜一些）：

• 第一步：構造兩個與非門，每個輸入都連接到其中一個。

• 第二步：將第一步中的兩個與非門的輸出作為第三個與非門的輸入。

• 第三步：將原始輸入 A 和第一個與非門的輸出連接到第四個與非門，將原始輸入 B 和第二個與非門的輸出連接到第五個與非門。

• 第四步：最後，將第四個和第五個與非門的輸出連接到第六個與非門。

• 結果：第六個與非門的輸出就是異或門的結果。

3. 構造加法門

半加器（Half Adder）

半加器是一個簡單的加法器，它可以處理兩個位的加法，並產生和（sum）和進位（carry）。

• 和：使用一個異或門來生成和。

• 進位：使用一個與門來生成進位。

• 使用與非門構造這些基本門，然後將它們組合起來形成半加器。

全加器（Full Adder）

全加器考慮了來自低位的進位輸入。

• 第一步：構造兩個半加器，第一個處理 A 和 B，第二個處理第一個半加器的和與進位輸入 C。

• 和：第二個半加器的和輸出。

• 進位：兩個半加器的進位輸出通過一個或門連接。

• 使用與非門構造半加器和或門，然後組合它們形成全加器。

4. 構造減法門

半減器（Half Subtractor）

半減器處理兩個位的減法。

• 差：使用一個異或門生成差。

• 借位：使用一個與非門和非門來生成借位。

• 使用與非門構造異或門和其他所需邏輯，然後組合它們形成半減器。

全減器（Full Subtractor）

全減器考慮了來自高位的借位。

• 第一步：構造兩個半減器，第一個處理 A 和 B，第二個處理第一個半減器的差與借位輸入。

• 差：第二個半減器的差輸出。

• 借位：兩個半減器的借位輸出通過一個或門連接。

• 使用與非門構造半減器和或門，然後組合它們形成全減器。

5. 構造乘法門

二進制乘法

實現兩個二進制數的乘法。

• 第一步：使用與門進行位乘法。

• 第二步：使用全加器串聯進行連續的加法。

• 第三部：實現移位和累加。

6. 構造寄存器

D 觸發器

存儲一位二進制信息。

• 第一步：使用與非門創建鎖存器（Latch）。

• 第二步：將鎖存器擴展成觸發器（ Flip -flop）。

寄存器

存儲多位二進制數。

• 將多個 D 觸發器並行連接，每個存儲一位。

7. 構造時鐘

振蕩器

提供周期性的時鐘信號。

• 使用與非門創建反饋回路，產生連續的振蕩。

結論

與非門因其能夠構造任何其他邏輯門和復雜電路的能力而被稱為“通用邏輯門”。通過上述方法，可以利用與非門構建出復雜的加法、減法、乘法以及存儲和時鐘電路，這是計算機和數字系統中進行算術運算的基礎。在現代集成電路設計中，與非門因其簡單性和多功能性而廣泛使用。

在 B² Network 的實踐中，通過與非門可以構造任何的計算邏輯。

密碼學中的承諾

承諾在密碼學和區塊鏈中應用非常廣泛，像 SHA 256、Merkle Tree、零知識證明中的 KZG 都是承諾，像上文中介紹的 ZK-Rollup 將零知識證明作為 Rollup 的承諾，OP-Rollup 將虛擬機內的字節碼作為 Rollup 的承諾。

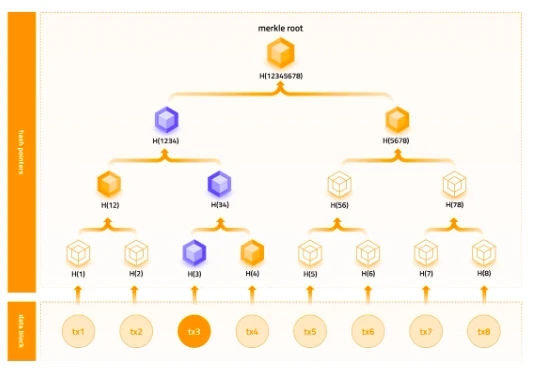
我們通過 Merkle Tree 來詳細說明如何使用承諾：

1. commit：Prover 將所有的 value 計算哈希，哈希作為二叉樹的葉子節點，不斷向上進行哈希計算，最終生成 Merkle Tree，發布 tree root hash 作為承諾。

2. reveal：Prover 揭露一個葉子節點對應的 value，以及其 branch。

3. check：Verifier 通過揭露的 value、branch 計算哈希，最終與發布的承諾進行對比，進行驗證。

如下圖示例：

1. commit：Prover 將 tx 1、tx 2 ……tx 8 分別計算哈希，獲得 H( 1)、H( 2)......H( 8)，不斷兩兩進行哈希計算，最終生成圖中的二叉樹結構，即 Merkle Tree，將 Merkle Tree 的 root 節點的值 H( 12345678)作為承諾進行發布。

2. reveal：Prover 揭露一個葉子結點對應的 value，如 tx 3 ，以及其 branch（H( 4) -> H( 12) -> H( 5678)）。

3. check：Verifier 通過揭露的 tx 3 和 branch（H( 4) -> H( 12) -> H( 5678)）進行計算並驗證承諾：

• 計算 tx 3 的哈希 H( 3)

• 將 H( 3)與 branch 中的 H( 4)進行哈希，得到 H( 34)

• 將 H( 34)與 branch 中的 H( 12)計算哈希，得到 H( 1234)

• 將 H( 1234)與 branch 中的 H( 5678)計算哈希，得到 H( 12345678)

• 將 H( 12345678)與公布的承諾進行驗證

B² Network 的零 知識證明驗證承諾

B² Network 是構建在比特幣網絡的 ZK-Rollup 二層解決方案。

Bitcoin 上 ZK-Rollup 的限制

由於比特幣的圖靈不完備限制，導致比特幣網絡上沒有辦法進行零知識證明的驗證，因此 ZK-Rollup 的傳統解決方案，在一層區塊鏈網絡驗證零知識證明的實現方式，是沒辦法在比特幣網絡上實現的。

ZK-Rollup 只將零知識證明和 Rollup 的數據聚合通過 Taproot 寫入比特幣網絡，只能保證 ZK-Rollup 的數據錨定在了比特幣網絡，無法被篡改，但是無法保證 ZK-Rollup 的交易的有效性、正確性，也沒辦法利用比特幣網絡的強大共識能力保證二層 ZK-Rollup 的安全性。

因此，一定需要在比特幣網絡上進行 ZK-Rollup 的確認。

零知識證明與算術電路

零知識證明

在零知識證明中，算術電路用於構建一個證明，證明者知道某些祕密信息，而不需要透露這些信息本身。

零知識證明使用算術電路生成證明：

• 生成證明

  一旦算術電路建立，證明者將使用他們的祕密輸入來計算電路的輸出。在這個過程中，證明者還會生成額外的信息（如零知識證明特有的承諾和隨機數），這些信息用於構建證明。

• 驗證證明

  證明者將他們的證明發送給驗證者。驗證者不知道證明者的祕密輸入，但他們有電路的描述和證明者的證明。驗證者通過執行電路的相同計算，並比較其結果與證明者提供的證明，來驗證證明的有效性。

算術電路

算術電路通常表示為一個有向無環圖（DAG），其中每個節點代表一個算術操作，邊代表操作之間的數據流。輸入節點代表電路的輸入值，通常是一些數字或變量，而內部節點代表算術操作。電路的輸出是最終的計算結果。

算術電路中的基礎電路門：

• 加法門（ Addition Gate）

• 乘法門（Multiplication Gate）

根據上文中與非門的介紹，算術電路是可以通過將加法門轉換為與非門，將乘法門轉換為與非門，最終算術電路轉換為基於與非門的邏輯門電路。

零知識證明驗證承諾

零知識證明的驗證程序本身是一個算術電路，通過將算術電路轉化為基於與非門的邏輯門，實際上可以將零知識證明的驗證程序轉化為基於與非門的邏輯門電路。

與非門通過比特幣腳本實現，將 Bit Value Commitment 作為輸入和輸出組裝成邏輯門，實現邏輯門約束。

可簡記為 OP_GATECOMMITMENT ，對應的 unlocking script 是 。

實際上，可以通過比特幣腳本實現與非門，再由與非門構造出加法門和乘法門，加法門和乘法門組合成算術電路，最終構造出零知識證明的驗證程序。但是由於涉及的門電路非常多，構造出的比特幣腳本也非常龐大，無法在比特幣網絡上真正運行。

將 Bit Value Commitment 作為輸入和輸出組裝成邏輯門，每一個帶有不同輸入和輸出的邏輯門作為葉子節點，組合成電路二叉樹，發布的 Circuit Taproot 是二叉樹的 root，減小了發布的尺寸。

Circuit Taproot 作為 B² Rollup 在一層區塊鏈網絡比特幣上提交的承諾。不同於傳統的 ZK-Rollup 可以在一層網絡執行驗證，B² Rollup 無法在比特幣上直接執行驗證。但是可以參考 Optimistic Rollup 的方式，針對承諾提供挑战機制，通過挑战機制完成 Circuit Taproot 承諾的確認。

驗證和響應協議

不同於 BitVM 需要提前籤署兩方間的鏈下交易。B² Network 採用發布鎖定獎勵的 UTXO 交易，解鎖腳本是一個 Taproot 腳本。

具體的解鎖 Taproot 腳本是 Prover 提前將 Circuit Taproot Tree 的每個 branch 生成腳本，並給定輸入的哈希。Challenger 利用 preimage 執行腳本，如果執行的 output 和 Prover 的提交不一致，就能利用 MAST （Taproot Merklized Abstract Syntax Tree，默克爾抽象語法樹）解鎖整個 Taproot，從而獲得鎖定的獎金。

由於零知識驗證程序的運行成本很小，也非常快速，因此比特幣網絡上的用戶都可以充當 Challenge 機制的觀察者，驗證 B² Rollup 提交的承諾，一旦發現承諾不一致，可以立即發起挑战。

挑战機制類似於 Arbitrum Rollup 的“交互式驗證遊戲”，不斷尋找錯誤執行的邏輯門計算。為了在衆多邏輯門中找到錯誤的一個，將會使用二分查找的方式，執行門電路比特幣腳本。最快找到錯誤分支的挑战者，可以在比特幣網絡上解鎖鎖定獎勵的 UTXO，從而獲得獎勵。

同時，Taproot 鎖定腳本中的一個分支是時間鎖腳本，當沒有 Challenge 成功挑战，Prover 將在挑战期結束後，通過時間鎖腳本解鎖 UTXO，取回獎勵。

總結

B² Network 通過 Ordinals Protocol，將 rollup 的 data 和 proof 聚合後寫入 Tapscript 中，利用不同的去中心化存儲協議保存 rollup 明細數據，有效地保證了 rollup 的 data availability。

B² Network 通過將 zero-knowledge proof verification commitment 記錄在 Bitcoin 上，允許任意的觀察者針對 commitment 進行挑战的機制，可以繼承 Bitcoin 的安全性，在 Bitcoin 上共識 rollup 的數據。

鄭重聲明：本文版權歸原作者所有，轉載文章僅為傳播信息之目的，不構成任何投資建議，如有侵權行為，請第一時間聯絡我們修改或刪除，多謝。