Perpetual Protocol是如何利用零和博弈原理魔改AMM的？
隨着 Layer 2 等擴容方案的逐步落地，最近衍生品賽道內的項目又重新引起了人們的關注，部分頭部項目的代幣價格也在近期連創歷史新高。這其中就包括在永續合約這個細分領域內長期佔據交易量第一的協議：Perpetual Protocol。
在上一篇《為什么永續合約是衍生品中最有前景的領域？》中，律動研究院曾重點討論了永續合約相比交割合約更適合鏈上交易環境的原因。本篇我們將重點分析 Perpetual Protocol 現行的 V1 版本的核心交易機制，詳細介紹衍生品市場與現貨市場的根本區別，以及 Perpetual Protocol 獨創的虛擬自動做市商（vAMM）機制的創新之處。
vAMM 並不是真正意義上的 AMM
傳統的 AMM 交易模式在現貨市場中已經有大量的成功案例，而無論其做市函數有多么特殊，每一個 AMM 平臺的基本組成結構也無非可以分成兩部分，那便是報價算法與資金池中的流動性，因此用公式可以表示為：
AMM 交易平臺 = AMM 自動報價算法 + 流動性提供者 (LP)
其中，AMM 自動報價算法有許多成熟的方案可供選擇，如 Perpetual Protocol 團隊所採用的 x*y = k 恆定乘積模型。但對於許多新生的 DeFi 協議來說，更為關鍵的問題往往是如何在發展早期獲取足夠的流動性支持。
不同於其他項目通過激勵機制對流動性進行購买，Perpetual Protocol 團隊在研發的過程中選擇主動繞开獲取流動性的問題，並進而开發了獨特的虛擬自動做市商機制，也就是我們所說的 vAMM。之所以稱其為虛擬 AMM，最主要的原因便是其組成結構中不再包括流動性提供者這個角色。
因此上方的公式也就可以修改為：
vAMM 交易平臺 = AMM 自動報價算法
在經過了以上大膽地刪改後，vAMM 平臺所剩的唯一功能，便是向交易者提供即時的報價服務。因此可以說，基於 vAMM 機制的 Perpetual Protocol V1 版本並不是傳統意義上的 AMM 交易平臺，平臺中也完全沒有真實的流動性，以及流動性提供者這個角色。自然，也沒有 LP 需要承擔無常損失之類的風險。
當然對交易者來說，平臺背後是不是真的存在流動性提供者其實完全沒有影響，交易體驗也與普通的 AMM 沒有什么區別。以下是在 Perpetual Protocol 上的 ETH/USDC 交易對進行交易的截圖，其組成部分按照順序分別是：
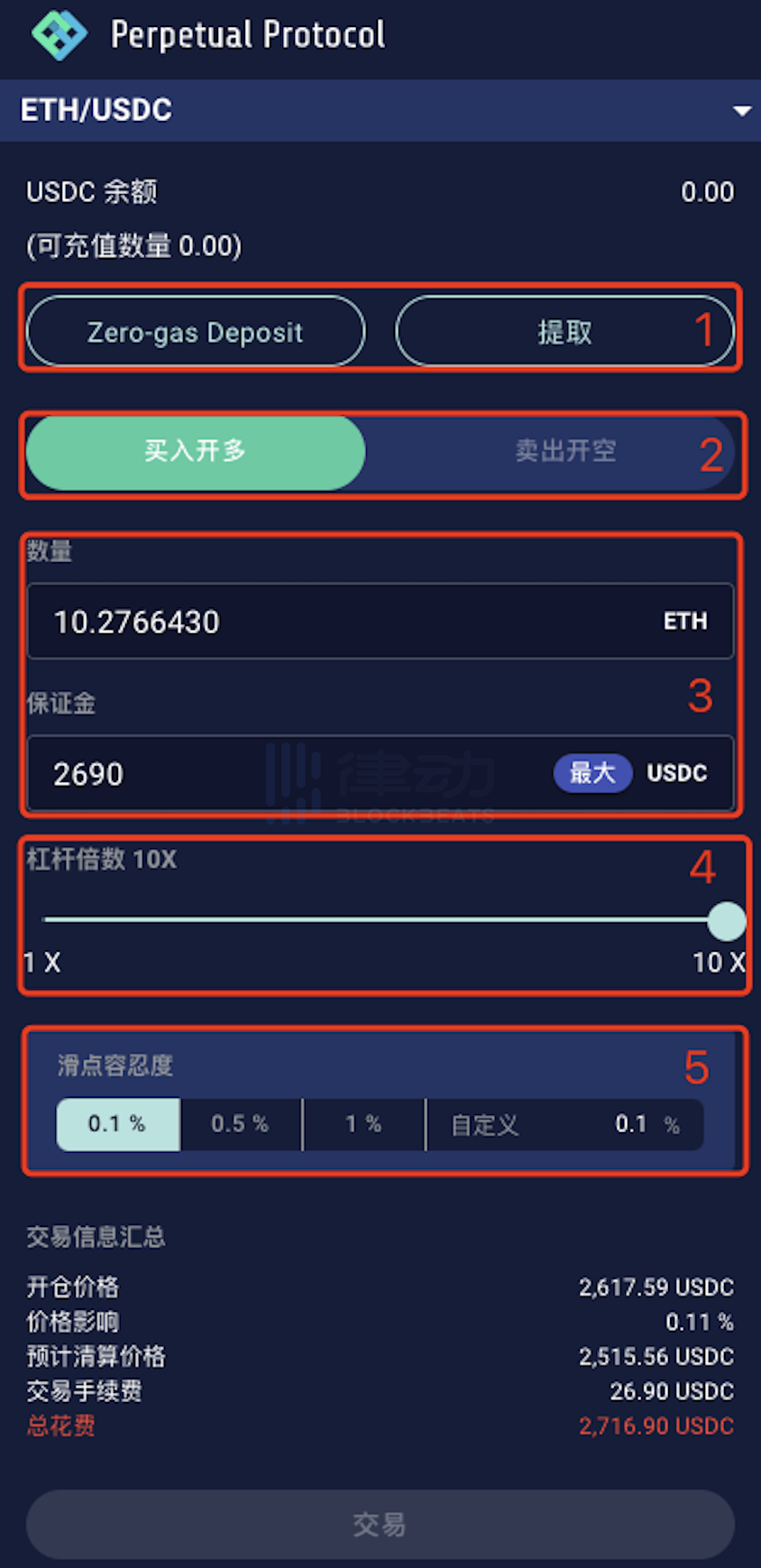
1. 存取保證金的按鈕：只有質押過一定數量的保證金才有資格开始交易；
2. 交易多空方向的選擇；
3. 交易的數量及佔用保證金的金額
4. 槓杆倍數（目前最大开放了十倍槓杆）
5. 交易者愿意承受的最高滑點；
可以看出，除了增加了保證金存取以及交易槓杆倍數的選擇外，在 Perpetual Protocol 上交易與 Uniswap 上的交易體驗基本沒有本質上的區別。這其實也是 Perpetual Protocol 協議最大的優勢，就是在不需要 LP 參與的情況下，卻能為用戶實現與現貨交易平臺相似的交易體驗。
只是，如果一個交易平臺內沒有真實的資金做市，那么這個平臺上的交易者，是從誰的手中購买資產，最後又把資產出售給誰？
想要理解這個問題，我們需要先明白衍生品市場與現貨市場的根本區別。
衍生品市場的基本特徵是零和博弈
零和博弈這個概念想必大多數讀者都聽說過，但是為什么有些市場是零和博弈的，而有些卻不是，可能許多讀者還並沒有認真地思考過這個問題。
現實中的衍生品市場，便是一個典型的零和博弈市場。我們以傳統金融中的期貨交易所為例，交易者在選擇做多或者做空時，必須找到相應的對手方與你同時進行反向的交易。因此在傳統的期貨市場中，每發生一筆交易，都會同時生成或銷毀一張多單和一張空單，或者轉移一張已經存在的多單或空單，這使得期貨市場會始終保持多單與空單數量的恆等。
因此任何一方的盈利，都必然對應着市場中另一方同樣額度的虧損。這便使得期貨市場成為了一個零和博弈市場，所有參與者只能通過繳納保證金入場博弈，並最終通過保證金結算盈虧，所得的利潤只會體現在保證金余額的增減上。
這種零和博弈雖然沒有增加社會整體的財富，但是卻具有其他的好處，那便是博弈不再需要真實的資產。因此傳統衍生品市場所需要的流動性，並不需要真實的資產，而是需要在市場中博弈者足夠多，使得任意一個參與方都能很容易地找到與自己交易方向相反的交易對手。
Perpetual Protocol 是如何構造零和博弈市場的
Perpetual Protocol 的博弈機制也與此類似，但是又有一些不同。
Perpetual Protocol 中的博弈者，在开立多單或空單的時候，不再需要一個與自己博弈方向相反的交易對手同時存在，而是直接與 vAMM 算法進行結算。為了繼續維持多空恆等式，這時便需要再引入一個新的維度，也就是時間。
由於 Perpetual Protocol 中的交易者不論最終取得盈利還是虧損，都需要將手中的頭寸進行平倉（平倉為最初开倉的反向交易），因此在 Perpetual Protocol 的 vAMM 交易市場中，所有的多空訂單保持着在時間層面的多空恆等關系。任何一個參與者在離場前，其在 vAMM 平臺中提交的多單數量與空單數量是恆等的。
這個特性給 Perpetual Protocol 協議帶來了許多其他交易平臺無法具有的優勢。比如不再需要對流動性進行激勵，不用考慮 LP 的無常損失問題，可以根據需求任意創建新的市場等等。
只是在享受這些優點的同時，vAMM 機制還有一個問題沒有解決，那就是 x*y=k 中 k 值的設定問題。
在 vAMM 中是如何決定 k 值的
在正常的 AMM 交易平臺中，k 值的大小完全不需要人為幹預，因為其大小只取決於資金池中真實流動性的多少。而在 vAMM 交易平臺中，由於沒有了真實流動性，x*y=k 中的 k 值該是多少，變成了一個需要管理者主觀判斷的問題。
在 Perpetual Protocol V1 採用的方案中，k 值是由項目團隊主動管理的。但人為設置 k 值卻是一個需要小心平衡的工作，如果 k 值設置得過大，則 vAMM 中的虛擬流動性便會過高，一筆交易對現有價格的影響變小。這自然能減少用戶在交易過程中承擔的滑點，但是一旦某個虛擬資金池中的交易者過少，而目標價格又變動過快，就很容易導致合約價格與目標價格脫錨，破壞永續合約的產品結構。而如果 k 值被設置的過低，又會使得該虛擬資金池的交易者承受更高的交易滑點，進而導致交易者的體驗下降。
這種設置工作無論是由中心化的團隊完成，還是通過社區治理投票決定，在效率與公平性上都有一定的缺陷。因此，如何將 k 值的設定工作盡快改為由市場或算法執行，成了 Perpetual Protocol 急需解決的問題。
在當前運行的版本中，k 值的設定會人為的參考相同交易對在 Uniswap 中的真實流動性大小，以真實的市場作為參考，能夠相對降低主觀判斷帶來的不利影響。Perpetual Protocol 的开發團隊也曾試圖开發“浮動 k 值”的自動算法。但團隊在權衡利弊之後，“浮動 k 值”的方案在 V2 版本的升級中被最終放棄。
我們將在下一篇中重點介紹 Perpetual Protocol V2 版本所採用的新版交易引擎，以及其在資本效率與平臺开放性上作出的重點改進。並且對比現貨交易平臺的發展軌跡，分析其是否有可能繼續成長為永續合約交易賽道的龍頭項目。
鄭重聲明：本文版權歸原作者所有，轉載文章僅為傳播信息之目的，不構成任何投資建議，如有侵權行為，請第一時間聯絡我們修改或刪除，多謝。